QUADRILATERI CIRCOSCRITTIBILI
Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:
- Poligoni circoscritti
- Quadrilateri circoscritti
- La circonferenza e il cerchio
- Quadrilateri
- Quadrato
- Rombo
Nella lezione precedente abbiamo visto che un QUADRILATERO può essere CIRCOSCRITTO ad una circonferenza se la SOMMA DEI LATI OPPOSTI è UGUALE.
Vediamo allora, tra i quadrilateri, quali sono circoscrittibili.
Può essere circoscritto ad una circonferenza il QUADRATO:
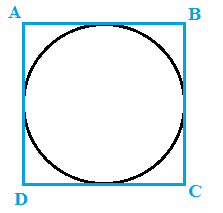
E' evidente, infatti che, poiché i LATI del quadrato sono tutti CONGRUENTI, la somma dei lati opposti è uguale, ovvero:
AB + DC = AD + BC.
Può essere circoscritto alla circonferenza anche il ROMBO:
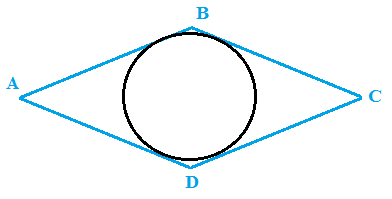
Anche i LATI del rombo sono tutti CONGRUENTI, e quindi la somma dei lati opposti è uguale, ovvero:
AB + DC = AD + BC.
