PROPRIETA' DELLE MATRICI AGGIUNTE
- Matrice
- Matrice quadrata
- Matrice identità
- Prodotto tra matrici
- Determinante di una matrice quadrata
- Matrice aggiunta
Nella lezione precedente abbiamo introdotto il concetto di MATRICE AGGIUNTA e abbiamo visto come essa può essere calcolata.
Ora vogliamo verificare la seguente uguaglianza:
A · agg(A) = agg(A) · det A = I
dove
A è la matrice data
agg(A) è la matrice aggiunta di A
det A è il determinante della matrice A
I è la matrice identità.
Consideriamo la matrice A
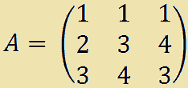
e la sua aggiunta che abbiamo calcolato nella lezione precedente
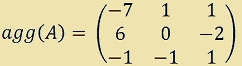
Ora calcoliamo il determinante di A:
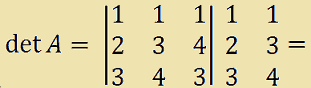
[(1 · 3 · 3) + (1· 4 · 3) + (1 · 2 · 4)] +
- [(1 · 3 · 3) + (1 · 4 · 4) + (1 · 2 · 3)] =
= [9 + 12 + 8] - [9 + 16 + 6] =
= 29 - 31 = -2.
Ora eseguiamo il prodotto della matrice A per la sua aggiunta:
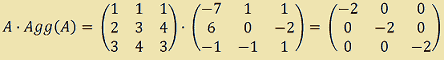
E' evidente che la matrice ottenuta non è altro che il prodotto del determinante di A, ovvero 2, per la matrice identità. Infatti:
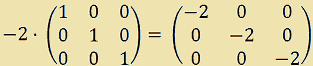
Ora eseguiamo il prodotto della matrice aggiunta di A per A.
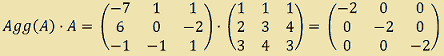
Anche in questo caso la matrice ottenuta non è altro che il prodotto del determinante di A, ovvero -2, per la matrice identità.






