MATRICI TRASPOSTE
Consideriamo una matrice A: si potrà trattare sia di una matrice quadrata che di una matrice con un numero di righe diverso dal numero delle colonne.
Esempio:
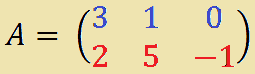
Ora SCAMBIAMO tra loro ordinatamente le RIGHE con le COLONNE e indichiamo la matrice ottenuta con AT. Avremo:
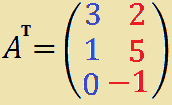
La trasformazione che abbiamo fatto prende il nome di TRASPOSIZIONE e la matrice che abbiamo ottenuto è detta MATRICE TRASPOSTA di A.
Come si nota la MATRICE TRASPOSTA è indicata con il simbolo AT (che si legge trasposta di A). In alcuni testi è possibile trovare anche il simbolo A'.
Se indichiamo con
aij
il generico elemento della matrice A
e con
a'ij
il generico elemento della matrice AT,
possiamo dire che
a'ij = aji
che si legge
a primo con i con j è uguale ad a con j con i.
Ad esempio, nella matrice precedente AT, l'elemento a21, è uguale a 1. Esso è uguale all'elemento a12 della matrice A.
Come possiamo notare dall'esempio precedente
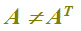
che si legge
A diversa da A con T.
In altre parole la MATRICE A è DIVERSA dalla sua TRASPOSTA.
Vi è un solo caso nel quale una matrice è uguale alla sua trasposta: è il caso in cui la matrice data è una matrice SIMMETRICA.
Ricordiamo che una matrice si dice SIMMETRICA se si tratta di una MATRICE QUADRATA i cui elementi soddisfano la condizione
aij = aji
con
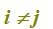
Esempio:
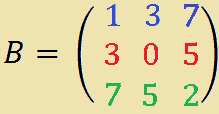
Quella che abbiamo scritto è una matrice simmetrica. Ora scriviamo la sua trasposta BT:
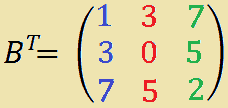
Come possiamo notare la trasposta di B è uguale alla matrice B.
Nella prossima lezione vedremo quali sono le proprietà delle trasposte.






