PROPRIETA' DELLE MATRICI TRASPOSTE
Dopo aver parlato, nella lezione precedente, delle MATRICI TRASPOSTE, in questa lezione ci occuperemo delle PROPRIETA' delle MATRICI TRASPOSTE.
Iniziamo col considerare un VETTORE COLONNA, ovvero una matrice formata da m righe ed UNA SOLA COLONNA.

La TRASPOSTA della matrice A è una MATRICE RIGA, cioè una matrice formata da UNA SOLA RIGA ed n colonne:
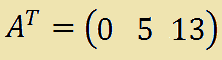
Allo stesso modo possiamo dire che la TRASPOSTA di un VETTORE RIGA è un VETTORE COLONNA.
Vediamo di seguito le PROPRIETA' DELLE TRASPOSTE:
(AT)T = A
(A + B)T = AT + BT
(k · A)T = k · AT
(A · B)T = BT ·AT.
In particolare, per quanto riguarda quest'ultima proprietà possiamo dire che la TRASPOSTA di un PRODOTTO si può ottenere come PRODOTTO delle SINGOLE TRASPOSTE considerate nell'ORDINE INVERSO. Ovvero
(A · B · C · D)T =DT · CT · BT · AT.






