MATRICI SIMMETRICHE
Si dice MATRICE SIMMETRICA una MATRICE QUADRATA i cui elementi soddisfano la condizione
aij = aji
con
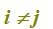
che si legge
a con i con j è uguale ad a con j con i
con i diverso da j.
Cerchiamo di capire cosa significa.
Iniziamo col ricordare che
a è il generico elemento della matrice
i indica la riga
j indica la colonna.
Mentre gli elementi tali che
i = j
sono gli elementi della DIAGONALE PRINCIPALE.
Ora immaginiamo di avere una matrice quadrata di 4 righe e 4 colonne. Essa sarà:
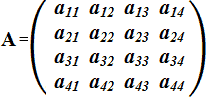
Ora gli elementi della DIAGONALE PRINCIPALE possono assumere qualsiasi valore. Ad esempio:
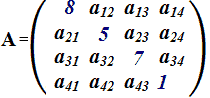
Gli altri elementi devono essere tali che
aij = aji.
Ad esempio se
a12 = 4
allora
a21 = 4.
Quindi:
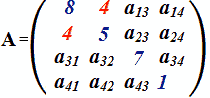
Se
a13 = 3
allora
a31 = 3.
Quindi:
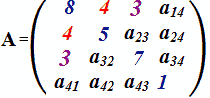
Se
a14 = 1
allora
a41 = 1.
Quindi:
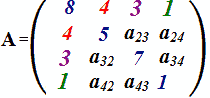
Se
a23 = 0
allora
a32 = 0.
Quindi:
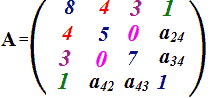
Se
a24 = -1
allora
a42 = -1.
Quindi:
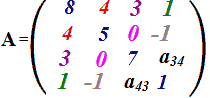
Se
a34 = 6
allora
a43 = 6.
Quindi:

Quella che abbiamo scritta sopra è una MATRICE SIMMETRICA.






