FUNZIONE DISPARI
Consideriamo la seguente FUNZIONE:
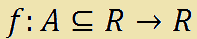
che si legge
f di A, contenuto o uguale ad R, in R.
Essa si dice DISPARI se per
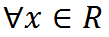
che si legge
qualunque x appartenente ad R
si ha:
f(x) = -f(-x)
che si legge
f di x è uguale a meno f di meno x.
Esempio:
y = x3
che si legge
y uguale ad x alla terza.
Iniziamo col vedere qual è il CAMPO DI ESISTENZA di questa funzione. Esso è dato da tutte le x appartenenti ai reali. Ovvero:
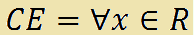
che si legge
campo di esistenza è uguale a qualsiasi x appartenente ai reali.
Assegniamo alla x alcuni valori per poter tracciare il grafico della funzione:
| x | y |
|---|---|
| 1 | 1 |
| 2 | 8 |
| 3 | 27 |
| -1 | -1 |
| -2 | -8 |
| -3 | -27 |
Disegniamo la nostra funzione:
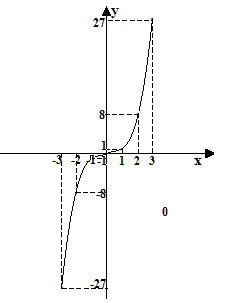
Come possiamo notare:
- se alla x diamo il valore di 1 la y vale 1;
- se alla x diamo il valore di -1 la y vale -1;
- se alla x diamo il valore di 2 la y vale 8;
- se alla x diamo il valore di -2 la y vale -8;
E così per tutti i numeri reali. Quindi il segno della y cambia al cambiare del segno della x.
Una funzione di questo tipo si dice FUNZIONE DISPARI.
Il GRAFICO di una FUNZIONE DISPARI è SIMMETRICO rispetto all'ORIGINE DEGLI ASSI.






