DISEQUAZIONI CON VALORE ASSOLUTO ED UNA COSTANTE
- I numeri relativi
- Valore assoluto: concetti base
- Nozione di valore assoluto
- Disequazioni con valore assoluto
- Disequazioni con valore assoluto e una costante
Nella lezione precedente abbiamo visto come si risolvono le disequazioni del tipo:
|A(x)| > k
oppure
|A(x)| ≥ k
dove k è una costante.
In questa lezione, invece, andremo a vedere come si risolvono disequazioni del tipo
|A(x)| < k
oppure
|A(x)| ≤ k
sempre con k costante.
Anche in questo caso, così come abbiamo visto nella lezione precedente, bisogna procedere in modo diverso a seconda che k sia un numero negativo oppure un numero positivo.
Partiamo dal caso in cui
k < 0.
A primo membro abbiamo un valore assoluto: esso è sempre positivo, quindi non sarà mai minore o uguale ad un numero negativo. Anche nel caso in cui la x dovesse assumere dei valori tali che A(x) è uguale a zero, la disequazione non è vera dato che lo zero è maggiore di un numero negativo.
In altre parole una disequazione simile non è MAI VERIFICATA. Possiamo anche scrivere:
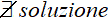
che si legge
non esiste soluzione
oppure
S = Ø
che si legge
la soluzione è l'insieme vuoto.
Esempio:
|6x + 8| < -3.
Nel nostro esempio
k = -3
quindi un valore negativo. Il primo membro è sempre positivo e, quindi, sempre maggiore del secondo. La disequazione non è mai verificata.
Vediamo un altro esempio:
|4x| ≤ -2.
Il primo membro è sempre positivo e non potrà mai essere minore del secondo membro che è negativo. Se il primo membro si annullasse (cosa che accade quando x = 0) avremmo
0 ≤ - 2
che non è mai vera. Quindi la nostra disequazione non ammette soluzioni.
Passiamo ad esaminare il caso in cui
|A(x)| ≤ k
con
k > 0.
Così come abbiamo fatto nella lezione precedente, anche in questo caso andiamo a considerare il VALORE ASSOLUTO di un numero o di una espressione come la sua DISTANZA DALL'ORIGINE di una linea dei numeri.
Come abbiamo già detto, dato il numero reale k, la sua distanza dall'origine è k. Ma anche il numero -k ha come distanza dall'origine k. Ovvero:
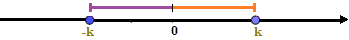
Ora, affinché un'espressione sia minore di k la sua distanza dall'origine deve essere minore rispetto alla distanza 0k oppure la sua distanza dall'origine deve essere minore rispetto alla distanza -k0.
Ad esempio questo si verifica quando:
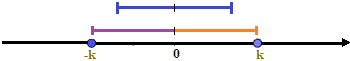
In altre parole, questo si verifica ogni volta che la nostra espressione si colloca nell'area tratteggiata del grafico:
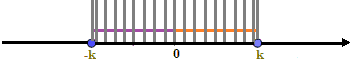
cioè ogni volta in cui A(x) è compreso tra k e - k.
In altre parole le soluzioni della disequazione sono
- k≤ A(x) ≤ k.
Chiaramente, se la disequazione è del tipo
|A(x)| ≤ k
la soluzione sarà
- k≤ A(x) ≤ k
mentre, se la disequazione è del tipo
|A(x)| < k
a soluzione sarà
- k < A(x) < k.
Esempio:
|2x - 3 | < 1.
Il verso della disequazione è minore e k è un numero positivo, 1 quindi si tratta di risolvere
-1 < 2x - 3 < 1.
Risolviamo separatamente le due disequazioni e alla fine andiamo a prendere i valore interni all'intervallo trovato:
2x - 3 > -1
2x - 3 < 1.
Risolviamo la prima
2x - 3 > -1
2x > -1 + 3
2x > 2
x > 1.
Passiamo alla seconda
2x - 3 < 1
2x < 1 + 3
2x < 4
x < 2.
La soluzione cercata è:
1 < x < 2.
Questa disequazione, può essere risolta anche con altri procedimenti: se volte sapere come, vi rimandiamo all'approfondimento Risoluzione di disequazioni con valore assoluto e costante.






