DISEQUAZIONI CON VALORE ASSOLUTO E LO ZERO
- I numeri relativi
- Valore assoluto: concetti base
- Nozione di valore assoluto
- Disequazioni con valore assoluto
Iniziamo a vedere come si risolvono i vari tipi di DISEQUAZIONI CON VALORE ASSOLUTO.
Partiamo dal caso in cui la disequazione si presenti in una delle forme seguenti:
|A(x)| > 0
|A(x)| < 0.
Ovviamente:
- anziché il simbolo di maggiore potremmo avere quello di maggiore o uguale;
- come, anziché il simbolo di minore potremmo avere quello di minore o uguale.
Partiamo dal caso:
|A(x)| > 0.
A primo membro abbiamo un valore assoluto: esso è sempre positivo, quindi la nostra disequazione è vera per qualunque x ad eccezione di quei valori di x che annullano A(x). Infatti se
A(x) = 0
il suo valore assoluto è uguale a zero e quindi il primo membro non sarà maggiore di zero.
In altre parole la soluzione è data da:
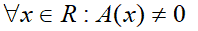
che si legge
qualunque x appartenente ai reali tale che A con x è diverso da zero.
Esempio:
|2x - 4| > 0.
La soluzione è data da qualunque x ad eccezione dei valori di x che annullano 2x - 4. Quindi poniamo
2x - 4 ≠ 0.
Risolviamo e abbiamo
2x ≠ 4
x ≠ 4/2
x ≠ 2.
La soluzione quindi è data da qualunque valore di x diverso da 2. Quindi la soluzione è
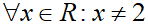
che si legge
qualunque x appartenente ai reali con x diverso da 2.
Passiamo al caso:
|A(x)| ≥ 0.
A primo membro abbiamo un valore assoluto: esso è sempre positivo, quindi la nostra disequazione è vera per qualunque x. In questa ipotesi non bisogna escludere le x che annullano A(x) dato che, quando esso si annulla, la disequazione è comunque verificata essendo presente anche il segno di uguaglianza.
Esempio:
|3x| ≥ 0.
La disequazione è vera per qualunque x appartenente ai reali, ovvero
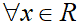
che si legge
qualsiasi x appartenente ai reali.
Vediamo ora il caso:
|A(x)| < 0.
A primo membro abbiamo un valore assoluto: esso è sempre positivo, quindi la nostra disequazione non è mai verificata dato che il primo membro non potrà mai essere minore di zero.
Esempio:
|5x + 2| < 0.
La disequazione non ammette soluzione. Quindi diremo che
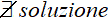
che si legge
non esiste soluzione
oppure diremo che
S = Ø
che si legge
la soluzione è l'insieme vuoto.
E se la disequazione si presenta nella forma
|A(x)| ≤ 0.
In questo caso la disequazione è vera solamente per quei valori di x che annullano A(x).
Esempio:
|5x + 2| ≤ 0.
La disequazione è vera solamente se
5x + 2 = 0.
Risolviamo e abbiamo
5x + 2 = 0
5x = -2
x = -2/5.
La soluzione della disequazione è quindi x = -2/5.






