FIGURE GEOMETRICHE ISOPERIMETRICHE ED EQUIVALENTI
- Poligoni equivalenti
- Figure geometriche equivalenti e figure geometriche congruenti
- Perimetro di un poligono
Nelle lezioni precedenti abbiamo appreso che DUE FIGURE GEOMETRICHE che hanno la STESSA AREA si dicono EQUIVALENTI.
Invece, due figure geometriche aventi il PERIMETRO della STESSA LUNGHEZZA si dicono ISOPERIMETRICHE.
Ora vogliamo chiederci se due poligoni equivalenti sono anche isoperimetrici e viceversa. In altre parole, se due poligoni hanno la stessa area hanno anche lo stesso perimetro? E se due poligoni hanno lo stesso perimetro questo significa che hanno anche la stessa area?
Partiamo da due figure geometriche CONGRUENTI, cioè due figure che sovrapposte l'una all'altra coincidono:
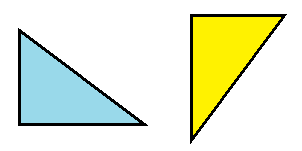
Poiché sovrapponendo la prima figura alla seconda esse coincidono è evidente che le due figure sono sia EQUIVALENTI che ISOPERIMETRICHE.
Ora esaminiamo due poligoni NON CONGRUENTI, ma EQUIVALENTI.
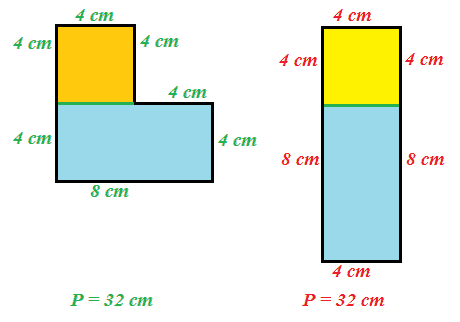
Come possiamo notare le due figure sono equivalenti
poiché sono equicomposte, cioè
composte dallo stesso numero di parti congruenti. Esse sono anche
isoperimetriche.
Ora esaminiamo altre due figure non congruenti, ma equivalenti:
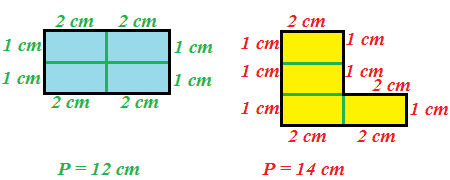
In questo caso le due figure sono equivalenti poiché sono equicomposte, ma non sono anche isoperimetriche.
Quindi possiamo affermare che figure geometriche EQUIVALENTI NON NECESSARIAMENTE sono anche ISOPERIMETRICHE.
Infine esaminiamo due poligoni NON CONGRUENTI, ma ISOPERIMETRICI.
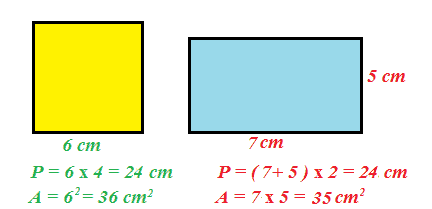
Come possiamo notare le due figure non sono equivalenti pur essendo isoperimetriche.
Quindi possiamo affermare che figure geometriche ISOPERIMETRICHE NON NECESSARIAMENTE sono anche EQUIVALENTI.
Concludendo possiamo dire che:
- POLIGONI CONGRUENTI sono anche EQUIVALENTI ed ISOPERIMETRICI;
- POLIGONI EQUIVALENTI non sono necessariamente CONGRUENTI ed ISOPERIMETRICI;
- POLIGONI ISOPERIMETRICI non sono necessariamente CONGRUENTI ed EQUIVALENTI.






