CONVERTIRE IN RADIANTI GLI ANGOLI ESPRESSI IN GRADI SESSAGESIMALI E VICEVERSA
- Nozione di angolo
- Come si misura l'ampiezza di un angolo
- Introduzione al concetto di radiante
- Il radiante
- Ampiezza degli angoli in radianti
Nella lezione precedente abbiamo visto che
| ANGOLO | MISURA IN GRADI SESSADECIMALI | MISURA IN RADIANTI |
|---|---|---|
| Angolo giro | 360° | 2π |
| Angolo piano | 180° | π |
| Angolo retto | 90° | π/2 |
Ma se avessimo un angolo di 32° o di 70° come faremmo a convertirlo in radianti?
E' abbastanza semplice dato che sappiamo che un angolo di 360°, in radianti misura 2π.
E' sufficiente, quindi, impostare la seguente proporzione:
α° : αrad = 360° : 2π
Da questa proporzione possiamo, data la misura dell'angolo in gradi α°, trovare la misura dell'angolo in radianti αrad. Infatti:
α° : αrad = 360° : 2π
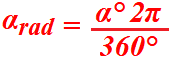
Così, ad esempio, l'angolo che nel sistema sessagesimale misura 32° in radianti misura:
αrad = (α°·2π)/360 = (32°·2π)/360 = 0,55850
Ricordiamo che π = 3,14159....
Mentre, se l'angolo nel sistema sessagesimale misura 70°, in radianti misura:
αrad = (α°·2π)/360 = (70°·2π)/360 = 1,22173
In questo modo possiamo trovare la misura in radianti di qualsiasi angolo espresso in gradi sessagesimali.
Attenzione però. Nel caso in cui la misura dell'angolo espressa in gradi sessagesimali, contiene anche primi e secondi, occorrerà prima effettuare una conversione in gradi sessadecimali.
Esempio: vogliamo sapere la misura in radianti di un angolo di 30° 15' 40''.
Per prima cosa dobbiamo passare dai gradi sessagesimali ai gradi sessadecimali. Ovvero:
30° 15' 40'' = 30° + (15/60)° + (40/3.600)° = 30° + 0,25° + 0,01111° = 30,26111°.
A questo punto possiamo passare dai gradi sessadecimali ai radianti:
αrad = (α°·2π)/360 = (30,26111° · 2π)/360 = 0,52815
La stessa proporzione può essere usata per convertire i radianti in gradi sessagesimali. Infatti
α° : αrad = 360° : 2π
da cui otteniamo

Esempio: vogliamo sapere la misura in gradi di un angolo la cui ampiezza in radianti è 0,39270.
α° = (αrad · 360)/2π = (0,39270 · 360)/2π = 22,50°
Chiaramente il risultato ottenuto è in gradi sessadecimali. Se vogliamo possiamo convertire i gradi sessadecimali in gradi sessagesimali, ricordando che
1° è formato da 60 primi e da 3.600 secondi. Quindi avremo:
22° + 0,5° · 60' = 22° 30'.
Vediamo un altro esempio: vogliamo sapere la misura in gradi di un angolo la cui ampiezza in radianti è 3,96301.
α° = (αrad · 360)/2π = (3,96301 · 360)/2π = 227,06394°
Ora, volendo convertire i gradi sessadecimali in gradi sessagesimali, avremo:
227° + 0,6394° · 60' = 22° + 38,364'
227° + 2' + 0,364' · 60'' = 22'' (chiaramente il risultato è stato arrotondato)
227° 2' 22''.
Nella prossima lezione continueremo a parlare di conversione tra diverse unità di misura degli angoli.






