RETTANGOLO
- Classificazione dei quadrilateri
- Parallelogramma
- Proprietà del parallelogramma
- Angolo retto - angolo acuto - angolo ottuso
- Confronto di due angoli
- Poligoni equiangoli poligoni equilateri poligoni regolari
- Triangolo rettangolo
- Primo criterio di congruenza dei triangoli
Disegniamo di seguito un RETTANGOLO:

Il RETTANGOLO è un PARALLELOGRAMMA che ha tutti e quattro gli ANGOLI RETTI e quindi tra loro CONGRUENTI:

Poiché gli angoli del rettangolo hanno tutti la stessa ampiezza esso è un POLIGONO EQUIANGOLO.
Un lato qualsiasi del rettangolo può essere considerato la sua BASE:
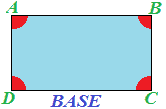
Uno dei lati ad esso perpendicolare sarà l'ALTEZZA del rettangolo:
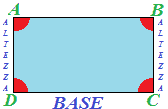
BASE e ALTEZZA sono dette anche DIMENSIONI del RETTANGOLO. Quindi possiamo dire anche che, DUE LATI CONSECUTIVI del rettangolo si dicono dimensioni del rettangolo:
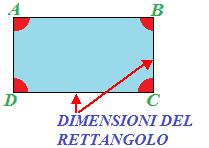
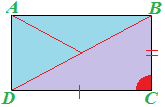
Disegniamo, ora, le DIAGONALI AC e BD del nostro rettangolo.
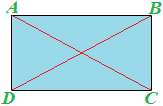
Ora consideriamo i due triangoli ottenuti ACD e BCD:
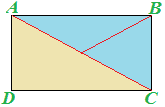
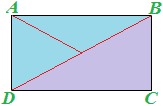
I due triangoli sono due TRIANGOLI RETTANGOLI dato che per definizione il rettangolo ha tutti angoli di 90°.
Poiché il RETTANGOLO è un parallelogramma, come tutti i parallelogrammi, i suoi LATI OPPOSTI sono CONGRUENTI.
Quindi il lato AD è congruente al lato BC:
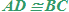
che si legge
AD è congruente a BC.
Questo significa che i due triangoli ACD e BCD hanno:
- un angolo della stessa ampiezza;
- due lati della stessa lunghezza.
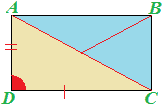
Il PRIMO CRITERIO DI CONGRUENZA dei TRIANGOLI ci dice che DUE TRIANGOLI sono CONGRUENTI se hanno rispettivamente CONGRUENTI DUE LATI e l'ANGOLO TRA ESSI COMPRESO come accade nel nostro caso.
Quindi essendo i due triangoli congruenti, anche le loro IPOTENUSE (AC e BD) sono CONGRUENTI. Ma le ipotenuse dei due triangoli sono le diagonali del rettangolo.
Questo significa che il RETTANGOLO ha le due DIAGONALI CONGRUENTI.
Essendo il RETTANGOLO un PARALLELOGRAMMA esso gode di tutte le PROPRIETA' dei parallelogrammi. Ovvero:
- ogni DIAGONALE divide il rettangolo in DUE TRIANGOLI CONGRUENTI; le DIAGONALI si TAGLIANO a META'. Inoltre, come abbiamo appena visto nel rettangolo le diagonali sono CONGRUENTI;
- i LATI OPPOSTI sono CONGRUENTI;
- come tutti i parallelogrammi gli angoli opposti sono congruenti. Nel rettangolo possiamo affermare che gli ANGOLI sono tutti RETTI e di conseguenza sono tutti CONGRUENTI (quindi non solo gli angoli opposti).






