MOLTIPLICAZIONE DI POLINOMI ORDINATI
- I polinomi
- Polinomi ordinati
- Prodotto di polinomi
- Moltiplicazione
- Monomi simili, monomi uguali, monomi opposti
Abbiamo visto nella lezione precedente che il PRODOTTO tra due POLINOMI è il polinomio i cui termini si ottengono MOLTIPLICANDO ogni TERMINE del primo POLINOMIO per ogni termine del secondo POLINOMIO.
Questo modo di procedere può risultare un po' complesso quando ci troviamo di fronte a polinomi con molti termini. In questi casi si può utilizzare un altro procedimento che ora andremo a spiegare.
Esempio:
(2x3 +4x2y + 7xy2 + 2y3) (2x2 - xy - y2).
Innanzitutto, per poter applicare il metodo che stiamo per vedere è necessario che tutte e due i polinomi siano ordinati secondo la medesima lettera.
Ricordiamo che un POLINOMIO si dice ORDINATO secondo le potenze decrescenti di una lettera, se i suoi TERMINI sono ORDINATI in modo che gli ESPONENTI di quella lettera vadano DECRESCENDO.
Nel nostro esempio i due polinomi sono ordinati secondo le potenze decrescenti della lettera x.
Ora scriviamo il primo polinomio (cioè il MOLTIPLICANDO) e il secondo polinomio (cioè il MOLTIPLICATORE) uno sotto all'altro. Così:
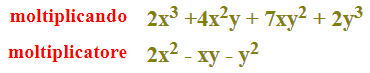
Iniziamo a scrivere, nella riga successiva, il PRODOTTO, tra il PRIMO TERMINE del MOLTIPLICANDO e il MOLTIPLICATORE. In altre parole moltiplichiamo 2x3 per ogni termine del moltiplicatore.
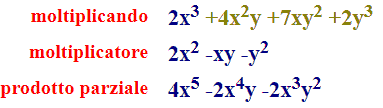
Abbiamo così ottenuto il primo PRODOTTO PARZIALE.
Ora scriviamo, nella riga successiva, il PRODOTTO, tra il SECONDO TERMINE del MOLTIPLICANDO e il MOLTIPLICATORE. In altre parole moltiplichiamo 4x2y per ogni termine del moltiplicatore.
E' importante, quando si scrive il secondo prodotto, METTERE IN COLONNA i TERMINI SIMILI, cioè aventi la stessa parte letterale. Notiamo, infatti, che il primo risultato ottenuto 8x4y lo poniamo sotto a -2x4y.
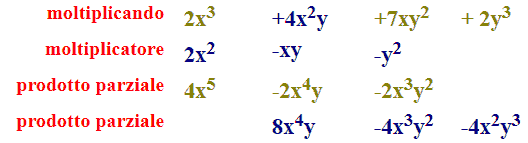
Abbiamo così ottenuto il secondo PRODOTTO PARZIALE.
Passiamo a scrivere, nella riga successiva il PRODOTTO, tra il TERZO TERMINE del MOLTIPLICANDO e il MOLTIPLICATORE. In altre parole moltiplichiamo 7xy2 per ogni termine del moltiplicatore.
Anche in questo caso dobbiamo METTERE IN COLONNA i TERMINI SIMILI. Il primo risultato ottenuto 14x3y2 lo poniamo sotto a -4x3y2.
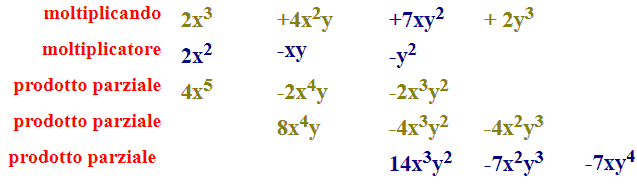
Infine MOLTIPLICHIAMO il QUARTO TERMINE del MOLTIPLICANDO e il MOLTIPLICATORE. In altre parole moltiplichiamo 2y3 per ogni termine del moltiplicatore.
Anche in questo caso dobbiamo METTERE IN COLONNA i TERMINI SIMILI.
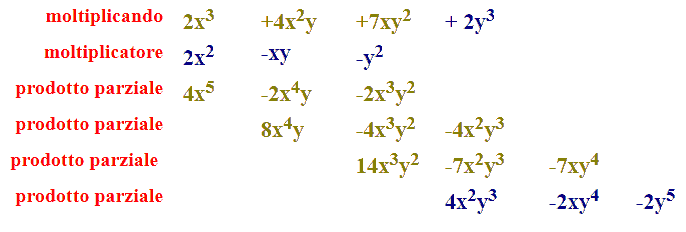
Ora non ci rimane che SOMMARE tra loro i vari PRODOTTI PARZIALI:
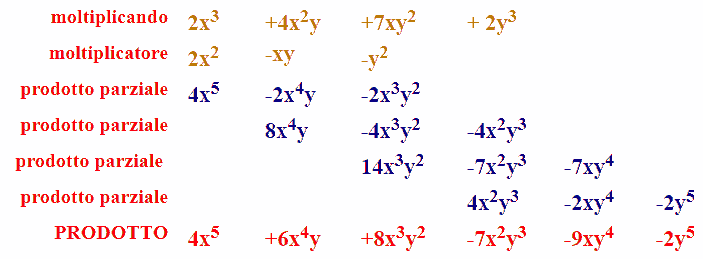
Abbiamo così ottenuto il nostro prodotto.
ATTENZIONE!!! Se il moltiplicatore o il moltiplicando o entrambi non sono polinomi COMPLETI bisogna LASCIARE dei POSTI VUOTI nei PRODOTTI PARZIALI in corrispondenza dei termini mancanti.
Esempio:
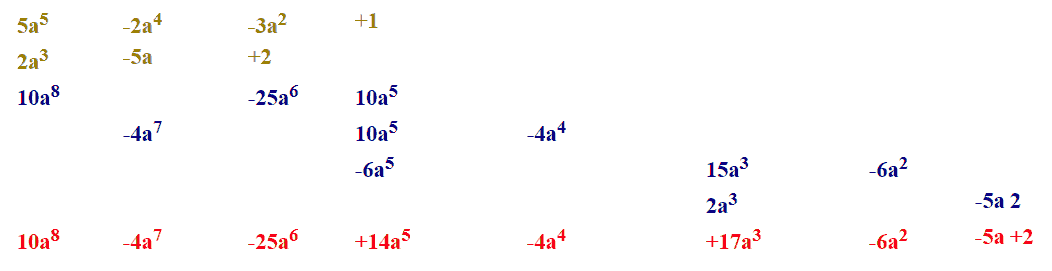
Nel moltiplicatore manca il termine con parte letterale a3e quello con parte letteralea , mentre nel moltiplicando mancano i termini con parte letterale a2 e a.






