COSTRUZIONE DI UN QUADRATO
- Quadrato
- La circonferenza e il cerchio
- Corde di una circonferenza
- Rette perpendicolari
- Angoli al centro
- Angolo retto - angolo acuto - angolo ottuso
- Poligoni equiangoli poligoni equilateri poligoni regolari
In questa e nelle prossime lezioni vedremo come è possibile costruire un poligono regolare.
In questa lezione inizieremo dalla COSTRUZIONE di un QUADRATO.
Iniziamo col disegnare una CIRCONFERENZA di centro O:
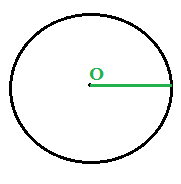
Ora disegniamo un DIAMETRO della circonferenza che chiamiamo DB:
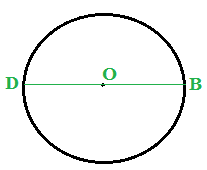
Ora disegniamo il DIAMETRO ad esso PERPENDICOLARE e lo chiamiamo AC:
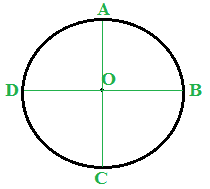
I quattro ANGOLI AL CENTRO che abbiamo disegnato sono congruenti e RETTI dato che li abbiamo ottenuti disegnando due diametri perpendicolari:
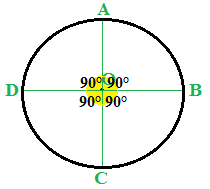
Noi sappiamo che, ad angoli al centro congruenti corrispondo ARCHI CONGRUENTI: quindi i quattro archi individuati dai due diametri disegnati, ed evidenziati sotto con colori diversi, sono congruenti.
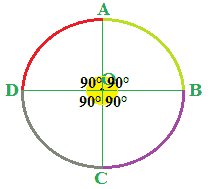
Quindi possiamo affermare di aver DIVISO la CIRCONFERENZA in 4 PARTI UGUALI.
Ora disegniamo le CORDE AB, BC, CD, DA:
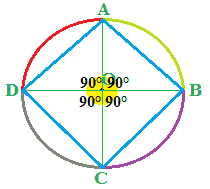
Le corde disegnate sono tutte congruenti, e sono anche i lati del poligono che di conseguenza è un poligono equilatero e, come abbiamo visto in una precedente lezione, anche equiangolo. Quindi abbiamo disegnato un poligono regolare con 4 lati, ovvero un QUADRATO.






