PROPRIETA' DELLE POTENZE
Vediamo, di seguito, quali sono le PROPRIETA' DELLE POTENZE.
Il prodotto di due o più potenze aventi la stessa base è una potenza della stessa base con esponente uguale alla somma degli esponenti.
Quindi:
am x an = a m+n
Esempio:
(3)2 x (3)3 = (9) x (27) = 243.
Come possiamo notare la base dei due fattori del prodotto è la stessa (3).
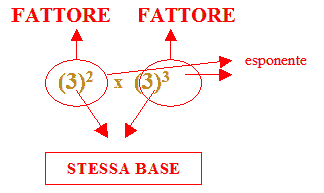
Ora proviamo ad applicare la regola precedente. Avremo:
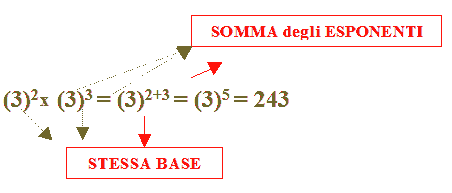
Come possiamo osservare il risultato è uguale.
Il quoziente di due o più potenze aventi la stessa base è una potenza della stessa base con esponente uguale alla differenza degli esponenti.
Quindi:
am : an = a m-n
ponendo come condizione che
m sia
maggiore di n
che si
scrive
m > n.
Esempio:
(2)4 : (2)3 = 16 : 8 = 2.
Come possiamo notare la base del dividendo e del divisore è la stessa (pari a 2).
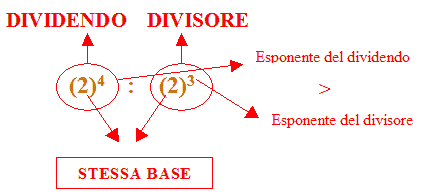
Ora proviamo ad applicare la regola precedente. Avremo:
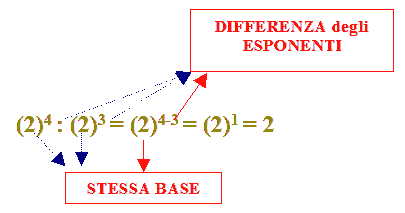
Come possiamo osservare il risultato è uguale.
La potenza di una potenza è una potenza che ha per base la stessa base e per esponente il prodotto degli esponenti.
Quindi:
(am)n = a mn
Esempio:
(42)3 = (16)3 = 4.096.
Ora proviamo ad applicare la regola precedente. Avremo:

Anche in questo caso il risultato è lo stesso.
Il prodotto tra due o più potenze aventi gli stessi esponenti è uguale ad una potenza che ha per base il prodotto delle basi e per esponente lo stesso esponente.
Quindi:
am x bm =(a b)m .
Esempio:
(2)2 x(3)2 = (4) x (9)= 36.
Come possiamo notare:
img class="immagine" src="../immagini_lezioni/lezione_03/im_06.png" alt="prodotto di potenze con uguale esponente">
Ora proviamo ad applicare la regola precedente. Avremo:

Anche in questo caso il risultato è lo stesso.
Il quoziente tra due potenze aventi gli stessi esponenti è uguale ad una potenza che ha per base il quoziente delle basi e per esponente lo stesso esponente.
Quindi:
am : bm =(a : b)m .
Esempio:
(8)2 : (2)2 = (64) : (4)= 16.
Ora proviamo ad applicare la regola precedente. Avremo:
Il risultato, come si può notare, è lo stesso.
- Esercizio 5 - Proprietà delle potenze
- Esercizio 6 - Proprietà delle potenze
- Esercizio 7 - Proprietà delle potenze






