FASCIO IMPROPRIO DI RETTE
- Retta parallela ad una retta data e passante per un punto
- Retta passante per l'origine degli assi
- Coefficiente angolare
- Equazione della retta
- Rette parallele
Si chiama FASCIO IMPROPRIO di rette un INSIEME di RETTE tutte PARALLELE tra loro.
Ad esempio:
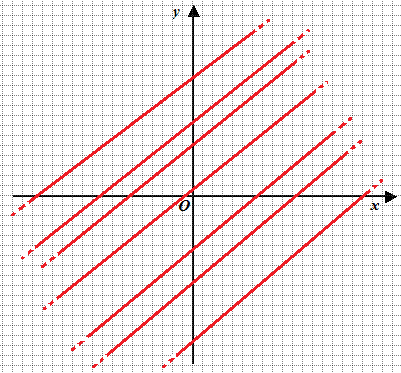
Quello che abbiamo disegnato è un FASCIO IMPROPRIO detto anche, più correttamente, FASCIO di RETTE PARALLELE.
Ovviamente, poiché queste rette sono tutte parallele, esse avranno tutte lo STESSO COEFFICIENTE ANGOLARE.
Quindi, data la generica equazione della retta:
y = mx + n
le rette di tale fascio avranno tutte lo stesso valore di m, mentre a variare sarà solamente il termine noto n: a seconda del valore da esso assunto avremo l'equazione di una retta o dell'altra.
Esempio 1:
scrivere il fascio di rette parallele alla retta
y = 2x + 8.
Il fascio di rette da noi cercato deve avere come coefficiente angolare 2.
Quindi esso sarà:
y = 2x + n.
Esempio 2:
scrivere il fascio di rette parallele alla retta
y = x + 3.
Il fascio di rette da noi cercato deve avere come coefficiente angolare +1, cioè il coefficiente della x che in questo caso è sottointeso.
Quindi esso sarà:
y = x + n.
Esempio 3:
scrivere l'equazione della retta passante per il punto P (3; 2) e appartenente al fascio improprio di rette di equazione
y = 2x +n.
Per prima cosa andiamo a cercare il valore di n. Lo facciamo sostituendo, nell'equazione del fascio improprio di rette, le coordinate di P:
y = 2x + n
2 = 2 · 3 + n
2 = 6 + n
- n = 6 - 2
- n = 4
n = -4.
La retta da noi cercata è
y = 2x - 4
visto che il coefficiente angolare deve essere lo stesso e il valore di n è -4.






