RETTA PARALLELA AD UNA RETTA DATA E PASSANTE PER UN PUNTO
- Equazione della retta
- Retta passante per l'origine degli assi
- Coefficiente angolare
- Fascio di rette passanti per un punto
- La retta
- Rette parallele
Disegniamo l'equazione di una generica retta r:
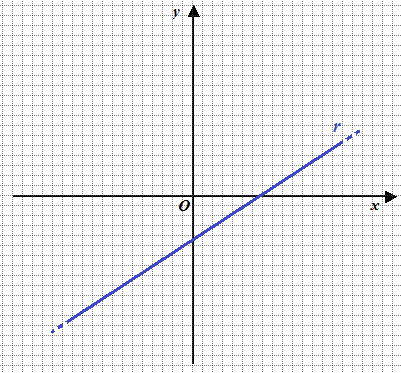
L'equazione di questa retta, come sappiamo, è:
y = mx + n.
Ora fissiamo, sul piano cartesiano un punto P0 tale che
P0 (x0; y0)
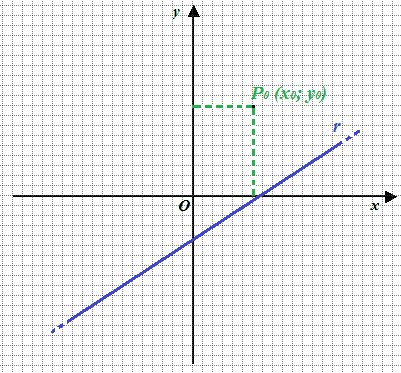
Ora vogliamo scrivere l'EQUAZIONE DELLA RETTA r', PARALLELA alla retta r e PASSANTE per il PUNTO P0:
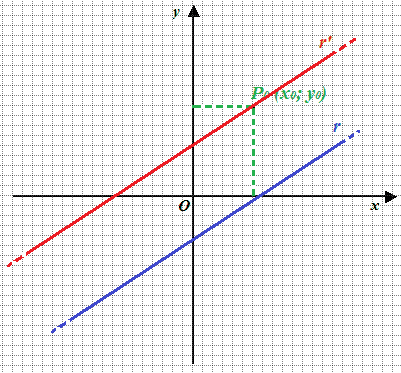
Dallo studio della geometria sappiamo che due RETTE sono PARALLELE quando esse NON HANNO ALCUN PUNTO IN COMUNE.
Perché ciò accada è necessario che le due rette, r e r', abbiamo la STESSA INCLINAZIONE, altrimenti ci sarebbe sempre un punto nel quale esse finirebbero con l'incontrasi.
Ma noi sappiamo che due rette hanno la stessa inclinazione quando hanno lo STESSO COEFFICIENTE ANGOLARE, dato che il coefficiente angolare di una retta indica l'inclinazione della retta rispetto all'asse delle ascisse.
Come possiamo fare, allora, per trovare l'equazione di una retta, r', parallela ad una retta data, r, e passante per il punto P0.
Iniziamo scrivendo il fascio di rette passanti per il punto P0, con la formula
y - y0 = m (x - x0).
Sappiamo che per ogni valore possibile di m, possiamo scrivere una diversa retta passante per P0 ed avente una certa inclinazione. Ma noi abbiamo detto che dobbiamo trovare la retta, r', che ha la stessa inclinazione di r, cioè che ha lo stesso coefficiente angolare, quindi basterà sostituire al fascio di rette passanti per P0, il coefficiente angolare della retta r.
Esempio:
scrivere l'equazione della retta passante per
P(1; -2)
e parallela alla retta di equazione
y = 3x + 1.
Iniziamo scrivendo il fascio di rette passanti per P:
y - y0 = m (x - x0)
y + 2 = m (x - 1).
Sostituiamo, al valore di m, il coefficiente angolare della retta data, ovvero 3. Avremo:
y + 2 = 3 · (x - 1)
y + 2 = 3x - 3
y = 3x - 3 - 2
y = 3x - 5.
Per verificare di aver trovato la soluzione giusta disegniamo le due rette. Partiamo dalla prima
y = 3x + 1
| x | y |
|---|---|
| 1 | 4 |
| 2 | 7 |
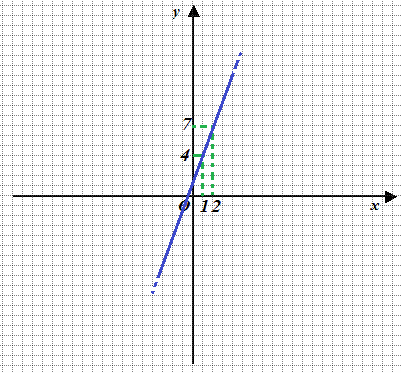
Ora disegniamo la seconda retta
y = 3x - 5
| x | y |
|---|---|
| 1 | -2 |
| 2 | 1 |
Già la tabella ci conferma che la retta passa per il punto P (1; -2):
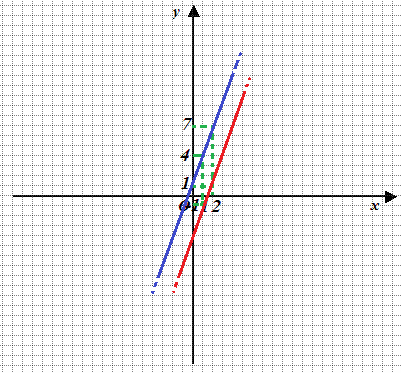
Le due rette sono parallele.






