PROBLEMI DEL TRE COMPOSTO: ESEMPI
- Costanti e variabili
- Problemi del tre composto
- Problemi del tre composto: come si risolvono
- Problemi del tre composto
Nella lezione precedente abbiamo visto come si risolvono i PROBLEMI DEL TRE COMPOSTO applicando il METODO DELLE PROPORZIONI.
Ora faremo qualche esempio di applicazione per rendere più chiaro il concetto.
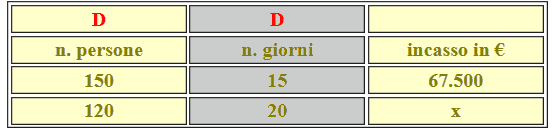
Un albergo ospita 150 persone per 15 giorni incassando complessivamente 67.500 euro. Quanto incassa successivamente per ospitare 120 persone per 20 giorni?
Risolviamo il problema:
- indichiamo con la lettera x la grandezza cercata, ovvero l'incasso per 120 persone per 20 giorni;
- costruiamo la tabella nella
quale riportiamo le nostre tre variabili: numero di persone, numero di
giorni, incasso:

- ora dobbiamo
stabilire se, ciascuna delle grandezze trovate è direttamente
o inversamente proporzionale
alla nostra incognita, lasciando invariati gli altri valori.
Partiamo dal numero di persone. A parità di giorni di permanenza in albergo, l''incasso è direttamente proporzionale al numero di persone.
Per ricordarcelo indichiamo una D, che sta ad indicare DIRETTAMENTE PROPORZIONALE, sulla prima colonna:

Passiamo al numero di giorni. Fermo restando il numero delle persone l'incasso è direttamente proporzionale al numero di giorni.
Per ricordarcelo indichiamo una D, che sta ad indicare DIRETTAMENTE PROPORZIONALE, sulla seconda colonna:
- Ora ricordiamo che il valore da noi
cercato è uguale al PRODOTTO
del VALORE NOTO di tale grandezza,
moltiplicato per i RAPPORTI DIRETTI dei
valori delle GRANDEZZE INVERSAMENTE PROPORZIONALI e
per i RAPPORTI INVERSI dei valori
DIRETTAMENTE PROPORZIONALI alla grandezza
di cui un valore è incognito.
Ovvero:
Quindi, l'albergo ospitando 120 persone per 20 giorni incassa 72.000 €.
Vediamo un altro esempio.
Una certa quantità di fieno è sufficiente a nutrire 8 cavalli, per 18 giorni dandone a ciascuno 24 kg al giorno. Per quanti giorni, la stessa quantità di fieno basterà per 12 cavalli, dandone a ciascuno 18 kg al giorno?
Risolviamo il problema:
- indichiamo con la lettera x la grandezza cercata, ovvero i giorni per i quali la stessa quantità di fieno è sufficiente per 12 cavalli dandone a ognuno 18 kg al giorno;
- costruiamo la tabella nella quale riportiamo le nostre tre variabili:
numero di cavalli, numero di giorni, kg al giorno per cavallo:

- ora dobbiamo
stabilire se, ciascuna delle grandezze trovate è direttamente
o inversamente proporzionale
alla nostra incognita, lasciando invariati gli altri valori.
Partiamo dal numero di cavalli. A parità di kg di fieno dati ad ogni cavallo il numero dei giorni è inversamente proporzionale al numero dei cavalli.
Inoltre a parità di numero dei cavalli il numero dei giorni è inversamente proporzionale ai kg di fieno somministrati giornalmente ad ogni cavallo.
Quindi:

- Ora ricordiamo che il valore da noi
cercato è uguale al PRODOTTO
del VALORE NOTO di tale grandezza,
moltiplicato per i RAPPORTI DIRETTI dei
valori delle GRANDEZZE INVERSAMENTE PROPORZIONALI e
per i RAPPORTI INVERSI dei valori
DIRETTAMENTE PROPORZIONALI alla grandezza
di cui un valore è incognito.
Ovvero:
Quindi, la stessa quantità di fieno basterà per 16 giorni se dobbiamo dare 18 kg di fieno al giorno a 12 cavalli.
Nella lezione successiva vedremo che i problemi del tre composto si possono risolvere anche con il metodo della riduzione all'unità, così come si è già detto per i problemi del tre semplice.






