COME RISOLVERE UN TRIANGOLO RETTANGOLO CONOSCENDO L'IPOTENUSA E UN ANGOLO ACUTO
- Relazioni trigonometriche per un triangolo rettangolo
- Secondo teorema dei triangoli rettangoli
- Risoluzione dei triangoli rettangoli
Concludiamo l'argomento relativo alla RISOLUZIONE DI UN TRIANGOLO RETTANGOLO esaminando il caso in cui sono noti l'IPOTENUSA e un ANGOLO ACUTO.
Come sempre lo facciamo attraverso un esempio.
Risolviamo il TRIANGOLO RETTANGOLO ABC, rettangolo in A
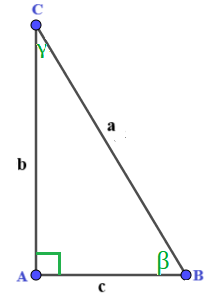
conoscendo i seguenti dati:
- ipotenusa CB = a = 24 cm;
- angolo acuto = β = 60°.
Per risolvere il triangolo rettangolo occorre determinare la misura dei due cateti e quella degli altri due angoli del triangolo.
Chiaramente, essendo un triangolo rettangolo, uno degli angoli ha l'ampiezza di 90°.
E poiché la SOMMA DEGLI ANGOLI INTERNI DI UN TRIANGOLO È PARI A 180°, l'angolo γ misura
180° - 60° - 90° = 30°.
A questo punto passiamo ai lati. Noi conosciamo la misura dell'ipotenusa e dobbiamo determinare la misura dei due cateti.
Il PRIMO TEOREMA DEI TRIANGOLI RETTANGOLI ci dice che LA MISURA DI UN CATETO E' UGUALE A QUELLA DELL'IPOTENUSA MOLTIPLICATA PER IL SENO DELL'ANGOLO OPPOSTO AL CATETO. Quindi, nel nostro caso, possiamo scrivere:
b = 24 · sen 60°
Il SENO DELL'ANGOLO DI 60° è pari a
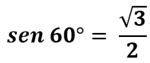
Quindi possiamo scrivere:
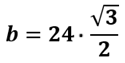
e semplificando abbiamo
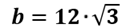
Ora dobbiamo determinare la misura dell'altro cateto. Possiamo farlo in due modi diversi:
- applicando il TEOREMA DI PITAGORA;
- oppure applicando di nuovo il PRIMO TEOREMA DEI TRIANGOLI RETTANGOLI.
Nel primo caso noi sappiamo che:
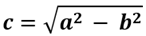
Da cui otteniamo
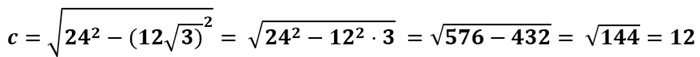
Invece, applicando di nuovo il primo teorema dei triangoli rettangoli e sapendo che LA MISURA DI UN CATETO E' UGUALE A QUELLA DELL'IPOTENUSA MOLTIPLICATA PER IL SENO DELL'ANGOLO OPPOSTO AL CATETO, avremo:
c = 24 · sen 30°
Poiché
possiamo scrivere:
c = 24 · 1/2 = 12
Ricapitolando, i risultati sono:
LATI:
a = 24;
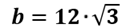
c = 12;
ANGOLI:
α = 90°;
β = 60°;
γ = 30°.






