DIVISIONE DI UN POLINOMIO PER UN MONOMIO
Vogliamo eseguire la seguente DIVISIONE di un polinomio PER un MONOMIO.
(8a3c - 16a2 +4ab) : (+4a).
Per prima cosa dobbiamo chiederci se, TUTTI i TERMINI del POLINOMIO sono DIVISIBILI per il MONOMIO dato.
Ogni termine del polinomio non è altro che un monomio e, parlando dei monomi, abbiamo appreso che affinché un MONOMIO sia DIVISIBILE per un altro è necessario che il DIVIDENDO contenga tutte le LETTERE che figurano nel DIVISORE e che esse siano elevate, ciascuna, ad un ESPONENTE MAGGIORE o almeno UGUALE a quello che figura nel DIVISORE.
Ricordiamo che:
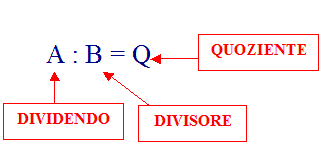
Nel nostro esempio:
- 8a3c è divisibile per 4a perché 8a3c contiene la lettera a con esponente superiore rispetto ad 1 (infatti nel monomio 4a, la lettera a ha come esponente 1);
- -16a2 è divisibile per 4a perché -16a2 contiene la lettera a con esponente superiore rispetto ad 1;
- 4ab è divisibile per 4a perché 4ab contiene la lettera a con esponente uguale ad 1.
Una volta appurato che tutti i termini del polinomio sono divisibili per il monomio per risolvere la nostra divisione applichiamo la PROPRIETA' DISTRIBUTIVA della DIVISIONE rispetto alla somma.
Tale proprietà ci dice che per DIVIDERE una SOMMA INDICATA per un NUMERO, basta DIVIDERE CIASCUN TERMINE DELLA SOMMA per QUEL NUMERO ed ADDIZIONARE tutti i QUOTI PARZIALI ottenuti.
Quindi, la nostra divisione può essere scritta anche così:
(8a3c - 16a2 +4ab) : (+4a) =
= (8a3c : 4a) + (-16a2 : 4a) + (4ab : 4a).
In questo modo non dobbiamo far altro che DIVIDERE ogni TERMINE del polinomio per il MONOMIO.
Quindi avremo:
(8a3c - 16a2 +4ab) : (+4a) =
= (8a3c : 4a) + (- 16a2 : 4a) + (4ab : 4a) =
= 2a2c + (-4a) + b
Quindi, quando un POLINOMIO è DIVISIBILE per un MONOMIO il quoziente è uguale al polinomio che si ottiene DIVIDENDO OGNI TERMINE del POLINOMIO per il MONOMIO.
Esempi:
| DIVISIONE | DIVISIBILI | RISULTATO |
|---|---|---|
| (a2x3 +6ax2 +10a3x) : (-2ax) | SI | -1/2ax2 -3x -5a2 |
| (10a2 +6a3b +5a5c) : (3a2) | SI | 10/3 +2ab +5/3a3c |
| (8ax2 -8a3x +4ax) : (-ax) | SI | -8x +8a2 -4 |
E se il POLINOMIO NON è DIVISIBILE per il MONOMIO? In questo caso non esiste un POLINOMIO QUOZIENTE che MOLTIPLICATO per il MONOMIO dia il DIVIDENDO.
Quindi, in questo caso, la divisione viene indicata come una FRAZIONE che ha al NUMERATORE il DIVIDENDO e al DENOMINATORE il DIVISORE. Quindi:

Esempio:
(2a2x3 -5ax2 +x) : (-2a3)
Il polinomio non è divisibile per il monomio perché, nonostante tutti i termini del primo contengano la lettera a, essa ha sempre un esponente minore rispetto a quello con il quale è presente nel dividendo.
Quindi la divisione va espressa nel modo seguente:
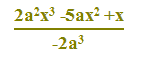
Tale frazione prende il nome di FRAZIONE ALGEBRICA.






