PUNTO DI INTERSEZIONE TRA DUE RETTE
- Punto di intersezione di due rette
- Punti di intersezione di una retta con gli assi cartesiani
- Retta parallela all'asse delle x
- Retta parallela all'asse delle y
- Sistemi di equazioni
- Risoluzione di un sistema di equazioni lineari
- Metodo di sostituzione
Nella lezione precedente abbiamo visto come è possibile individuare graficamente il PUNTO DI INTERSEZIONE di DUE RETTE: basta disegnare le due rette e individuare le COORDINATE del punto in cui esse si INCONTRANO.
Le COORDINATE del PUNTO DI INTERSEZIONE soddisfano entrambe le equazioni. Questo equivale a risolvere un SISTEMA di due EQUAZIONI di primo grado in due incognite, cioè cercare quei valori di x e di y che soddisfino contemporaneamente entrambe le equazioni.
In altre parole, date le equazioni
y = x + 1
y = - 2x -2.
Per trovare il punto di intersezione delle due rette possiamo anche risolvere il sistema:
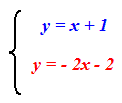
Risolviamo il sistema applicando uno dei metodi da noi conosciuti. In questo caso usiamo il metodo di sostituzione. In altre parole, risolviamo la prima equazione rispetto alla x e successivamente sostituiamo il valore trovato nella seconda.
Quindi avremo:
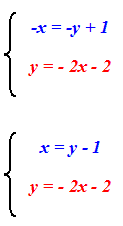
Ora andiamo a sostituire nella seconda il valore appena trovato della x e avremo:
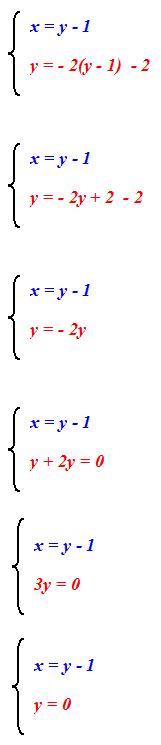
Infine, sostituiamo il valore della y appena trovato nella prima equazione:
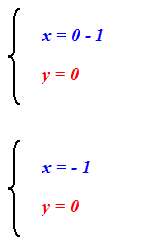
Quindi il punto di intersezione delle due rette è
P (-1 ; 0).
In altre parole siamo giunti, seguendo un'altro metodo, allo stesso risultato visto nella lezione precedente.
Questo modo di procedere può essere seguito anche per trovare i PUNTI DI INTERSEZIONE di una retta con gli ASSI CARTESIANI. Sarà necessario, in questo caso, risolvere due sistemi:
- il primo
comprendente la RETTA
data e l'EQUAZIONE dell'ASSE
delle x,
ovvero y
= 0.
La soluzione del sistema rappresenta l'intersezione della retta con l'asse delle x;
-
il secondo comprendente la RETTA data e l'EQUAZIONE dell'ASSE delle y, ovvero x = 0
La soluzione del sistema rappresenta l'intersezione della retta con l'asse delle x;






