ESERCIZI SULLE DISEQUAZIONI DI PRIMO GRADO
Esercizio 12
Risolvere la seguente disequazione:
x/2 + x/3 > 0.
Svolgimento
Per prima cosa dobbiamo liberare la disequazione dal denominatore. Per fare ciò, iniziamo a calcolare il minimo comune denominatore tra 2 e 3: esso è 6 e trasformiamo le due frazioni a primo membro in frazioni equivalenti con denominatore 6. Il secondo membro resta invariato dato che 0 : 6 = 0. Avremo:
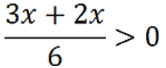
Eseguiamo la somma indicata a primo membro e otteniamo:
5x/ 6 > 0.
Moltiplichiamo per 6 primo e secondo membro e abbiamo:
5x > 0.
Ora dividiamo entrambi i membri per il coefficiente della x, ovvero per 5. Avremo:
x > 0/5.
Ma noi sappiamo che 0/5 è uguale a 0. Quindi il risultato della nostra disequazione è:
x > 0.
Vediamo, ora, come possiamo rappresentare il risultato ottenuto. Riportiamo, i vari metodi possibili:
x > 0
oppure
{x ∈ R : x > 0}
oppure
] 0 ; +∞ [
oppure

- Esercizio 1 - Esercizio sulle disequazione di primo grado intere
- Esercizio 2- Esercizio sulle disequazione di primo grado intere
- Esercizio 3 - Esercizio sulle disequazione di primo grado intere
- Esercizio 4 - Esercizio sulle disequazione di primo grado intere
- Esercizio 5 - Esercizio sulle disequazione di primo grado intere
- Esercizio 6 - Esercizio sulle disequazione di primo grado intere
- Esercizio 7 - Esercizio sulle disequazione di primo grado intere
- Esercizio 8 - Esercizio sulle disequazione di primo grado intere
- Esercizio 9 - Esercizio sulle disequazione di primo grado intere
- Esercizio 10 - Esercizio sulle disequazione di primo grado intere
- Esercizio 11 - Esercizio sulle disequazione di primo grado intere
- Esercizio 13 - Esercizio sulle disequazione di primo grado intere
- Esercizio 14 - Esercizio sulle disequazione di primo grado intere
- Esercizio 15 - Esercizio sulle disequazione di primo grado intere
- Esercizio 16 - Esercizio sulle disequazione di primo grado intere
- Esercizio 17 - Esercizio sulle disequazione di primo grado intere
- Esercizio 18 - Esercizio sulle disequazione di primo grado intere






