CALCOLO DEL PERIMETRO DEI QUADRILATERI
- Perimetro di un poligono
- Quadrilateri
- Perimetro dei quadrilateri
- Trapezio isoscele
- Parallelogramma
- Quadrato
- Figure geometriche equivalenti e figure geometriche congruenti
- La frazione di un numero
Nella lezione precedente abbiamo visto come si calcola il PERIMETRO dei vari QUADRILATERI.
Ora proveremo ad applicare le regole apprese ad alcuni casi concreti.
Esempio 1.
Un trapezio isoscele ha il lato obliquo che misura cm 12. La base minore è pari ai 2/3 del lato obliquo e la base maggiore è pari ai 5/4 del lato obliquo. Calcolare il perimetro.
Sappiamo che il TRAPEZIO ISOSCELE ha i LATI OBLIQUI CONGRUENTI.
Quindi per calcolare il perimetro è sufficiente determinare la lunghezza della base minore e della base maggiore.
Ricordando quanto appreso nello studio della frazioni, possiamo scrivere:
b1 = (12 : 3) x 2 = 8 cm (base minore)
b2 = (12 : 4) x 5 = 15 cm (base maggiore)
P = b1 + b2 + (l x 2) = 8 + 15 + (12 x 2)=
= 8 + 15 + 24 =47 cm (perimetro).
Esempio 2.
In un trapezio isoscele il perimetro è lungo m 66 ed uno dei lati obliqui misura m 15. Calcolare le misure delle basi, sapendo che l'una e doppia dell'altra.
Sappiamo che il TRAPEZIO ISOSCELE ha i LATI OBLIQUI CONGRUENTI e che il PERIMETRO è la SOMMA delle MISURE DELLE LUNGHEZZE di tutti i suoi LATI.
Se al perimetro sottraiamo la misura delle lunghezze dei due lati obliqui, otteniamo la somma delle due basi. Nel nostro caso avremo:
Somma delle basi = 66 - (15 x 2) =
= 66 - 30 = 36 m.
Poiché una base è doppia rispetto all'altra avremo:
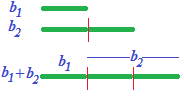
La base maggiore misura il doppio della base minore quindi, se dividiamo la misura della somma delle basi per 3, otteniamo la base minore. Pertanto:
b1 = 36 : 3 = 12 m (base minore).
La base maggiore misurerà il doppio della base minore. Cioè:
b2 = 12 x 2 = 24 m (base maggiore).
Esempio 3.
In un parallelogramma due lati consecutivi misurano cm 8 e cm 13. Calcolare il perimetro.
Sappiamo che il PARALLELOGRAMMA ha i LATI OPPOSTI CONGRUENTI.
Quindi per calcolare il perimetro è sufficiente fare la somma delle misure dei lati consecutivi e moltiplicare la somma ottenuta per 2.
P = (8 + 13) x 2 = 42 cm (perimetro).
Esempio 4.
Il perimetro di unquadrato è pari a cm 24. Determinare la misura del lato.
Sappiamo che il QUADRATO ha TUTTI i LATI CONGRUENTI.
Quindi per calcolare la misura del lato è sufficiente dividere il perimetro in 4 parti uguali: ognuna di esse rappresenta la lunghezza di un lato. Ovvero:
l = 24 : 4 = 6 cm (lato).






