TRAPEZIO: DEFINIZIONE
- Trapezio
- Trapezio isoscele
- Trapezio rettangolo
- Trapezio scaleno
- Rette parallele
- Gli angoli
- Angoli convessi
- Rette perpendicolari
Sappiamo che un TRAPEZIO è un QUADRILATERO che ha DUE LATI OPPOSTI PARALLELI.
Ma abbiamo visto anche che un TRAPEZIO può essere ottenuto da un TRIANGOLO tagliandolo con una RETTA PARALLELA alla BASE.
In questa lezione vedremo che esiste ancora un'altra definizione di trapezio.
Disegniamo DUE RETTE PARALLELE (a e b).
La PARTE di PIANO compresa tra DUE RETTE PARALLELE prende il nome di STRISCIA:
SOVRAPPONIAMO alla striscia appena disegnata un ANGOLO CONVESSO, (cioè un angolo che non contiene i prolungamenti dei suoi lati). Il VERTICE di tale angolo deve essere ESTERNO alla striscia.
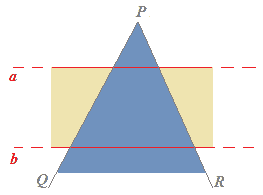
Come possiamo notare abbiamo disegnato
l'angolo convesso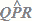 
il cui vertice 
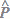è esterno alla striscia ab.
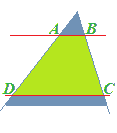
L'area delimitata dai punti ABCD rappresenta un trapezio:
-
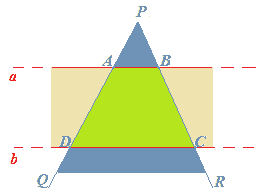
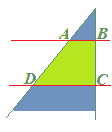
Se il LATO
DELL'ANGOLO è PERPENDICOLARE
rispetto alla STRISCIA
avremo un TRAPEZIO RETTANGOLO.
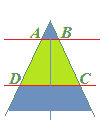
- Se la BISETTRICE
dell'ANGOLO è PERPENDICOLARE
alla STRISCIA avremo un TRAPEZIO
ISOSCELE.
Ricordiamo che la BISETTRICE di un angolo è la SEMIRETTA che ha per ORIGINE il VERTICE dell'angolo e che divide l'angolo in DUE PARTI UGUALI.
- In tutti gli altri casi avremo un TRAPEZIO
SCALENO.
