TRAPEZIO RETTANGOLO
- Trapezio
- Trapezio isoscele
- Trapezio scaleno
- Figure geometriche equivalenti e figure geometriche congruenti
- Rette perpendicolari
- Gli angoli
Un TRAPEZIO si dice RETTANGOLO se:
- i LATI OBLIQUI sono DISUGUALI;
- uno dei lati obliqui è PERPENDICOLARE alle BASI.
Disegniamo un TRAPEZIO RETTANGOLO:
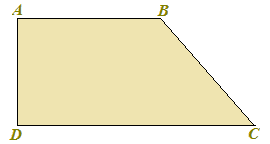
Notiamo che i lati obliqui AD e BC sono disuguali.
Inoltre il lato AD è perpendicolare alle basi AB e DC.
Il LATO OBLIQUO PERPENDICOLARE alle basi è anche l'ALTEZZA del trapezio. Nel nostro esempio il lato AD è anche l'altezza del nostro trapezio.
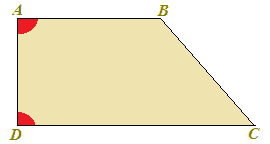
Essendo uno dei lati obliqui perpendicolare alle due basi, tale lato incontrandosi con la base maggiore e la base minore formerà due angoli retti. Quindi il TRAPEZIO RETTANGOLO ha sempre DUE ANGOLI RETTI.
Li abbiamo evidenziati, nella figura sottostante, in rosso.
Il TRAPEZIO RETTANGOLO ha una sola PROIEZIONE DEL LATO OBLIQUO sulla BASE MAGGIORE. Nel nostro caso essa è rappresentata dal segmento HC.
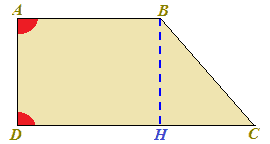
Come si nota nell'immagine il segmento HC è pari alla DIFFERENZA tra la BASE MAGGIORE e la BASE MINORE. Quindi:
HC = DC - AB.






