L'INSIEME DEI QUADRILATERI
- Quadrilateri
- Classificazione dei quadrilateri
- Rappresentazione grafica di un insieme
- Rappresentazione caratteristica di un insieme
- Sottoinsiemi di un insieme
- Intersezione di due insiemi
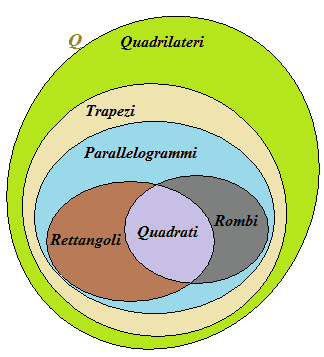
Vediamo, come è possibile, CLASSIFICARE I QUADRILATERI e rappresentarli utilizzando un DIAGRAMMA di VENN.
Sappiamo che un QUADRILATERO è un POLIGONO che ha QUATTRO LATI e QUATTRO ANGOLI.
Chiamiamo con Q l'INSIEME DEI QUADRILATERI e scriviamo:
QUADRILATERI = {poligoni | poligono ha 4 lati e 4 angoli}
che si legge
l'insieme dei QUADRILATERI formato dai poligoni tali che il poligono ha 4 lati e 4 angoli.
Ora rappresentiamo graficamente questo insieme con un DIAGRAMMA DI VENN:

Tra i POLIGONI che hanno 4 lati e 4 angoli ve ne sono alcuni che hanno UNA COPPIA DI LATI OPPOSTI PARALLELI. Essi prendono il nome di TRAPEZI.
Quindi:
TRAPEZI = {quadrilateri | quadrilatero ha una coppia di lati opposti paralleli}
che si legge
l'insieme dei TRAPEZI formato dai quadrilateri tali che il quadrilatero ha una coppia di lati opposti paralleli.
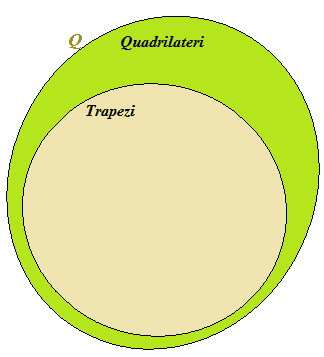
Poiché anche i trapezi hanno 4 lati e 4 angoli, l'insieme dei TRAPEZI è un SOTTOINSIEME dell'insieme dei QUADRILATERI.
Infatti un insieme B è SOTTOINSIEME di un INSIEME A se OGNI ELEMENTO di B è ANCHE ELEMENTO di A.
Quindi possiamo dire che
TRAPEZI è un SOTTOINSIEME di QUADRILATERI
scriveremo
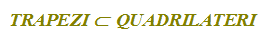
che si legge
l'insieme dei TRAPEZI è incluso nell'insieme dei QUADRILATERI.
Graficamente potremo disegnare i due insiemi nel modo che segue:
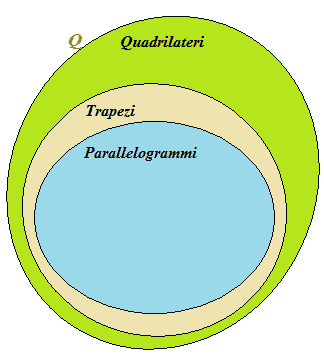
Tra i poligoni aventi 4 lati e 4 angoli (cioè tra i QUADRILATERI) ve ne sono alcuni che hanno ENTRAMBE LE COPPIE DI LATI OPPOSTI PARALLELE. Essi prendono il nome di PARALLELOGRAMMI.
Quindi:
PARALLELOGRAMMI = {quadrilateri | quadrilatero ha entrambe le coppie di lati opposti paralleli}
che si legge
l'insieme dei PARALLELOGRAMMI formato dai quadrilateri tali che il quadrilatero ha entrambe le coppie di lati opposti paralleli.
E' chiaro che, avendo il parallelogrammo entrambe le coppie di lati opposti paralleli, avrà anche una coppia di lati opposti paralleli. Quindi l'insieme dei PARALLELOGRAMMI è un SOTTOINSIEME dell'insieme dei TRAPEZI.
Quindi possiamo dire che
PARALLELOGRAMMI è un SOTTOINSIEME di TRAPEZI
scriveremo
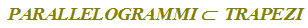
che si legge
l'insieme dei PARALLELOGRAMMI è incluso nell'insieme dei TRAPEZI.
Graficamente potremo disegnare i nostri insiemi nel modo che segue:
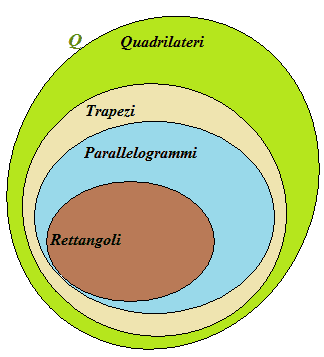
Tra i parallelogrammi, cioè tra i poligoni aventi quattro lati e quattro angoli e aventi entrambe le coppie di lati opposti paralleli, ve ne sono alcuni che hanno i QUATTRO ANGOLI CONGRENTI. Essi prendono il nome di RETTANGOLI.
Quindi:
RETTANGOLI = {parallelogrammi | parallelogramma ha i quattro angoli congruenti}
che si legge
l'insieme dei RETTANGOLI formato dai parallelogrammi tali che il parallelogramma ha i quattro angoli congruenti.
E' chiaro quindi che l'insieme dei RETTANGOLI è un SOTTOINSIEME dell'insieme dei PARALLELOGRAMMI.
Quindi
Tra i parallelogrammi, cioè tra i poligoni aventi quattro lati e quattro angoli e aventi entrambe le coppie di lati opposti paralleli, ve ne sono alcuni che hanno i QUATTRO LATI CONGRENTI. Essi prendono il nome di ROMBI.
Quindi:
ROMBI = {parallelogrammi | parallelogramma ha i quattro lati congruenti}
che si legge
l'insieme dei ROMBI formato dai parallelogrammi tali che il parallelogramma ha i quattro lati congruenti.
E' chiaro quindi che l'insieme dei ROMBI è un SOTTOINSIEME dell'insieme dei PARALLELOGRAMMI.
Quindi
Tra i parallelogrammi, cioè tra i poligoni aventi quattro lati e quattro angoli e aventi entrambe le coppie di lati opposti paralleli, ve ne sono alcuni che hanno i QUATTRO ANGOLI e i QUATTRO LATI CONGRENTI. Essi prendono il nome di QUADRATI.
Quindi:
QUADRATI = {parallelogrammi | parallelogramma ha i quattro angoli e i quattro lati congruenti}
che si legge
l'insieme dei QUADRATI formato dai parallelogrammi tali che il parallelogramma ha i quattro angoli e i quattro lati congruenti.
E' chiaro che l'insieme dei QUADRATI è un SOTTOINSIEME dell'insieme dei PARALLELOGRAMMI.
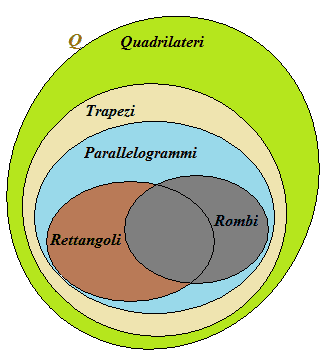
Ora immaginiamo di voler trovare l'INSIEME INTERSEZIONE dell'insieme dei RETTANGOLI e di quello dei ROMBI.
Come sappiamo, dati due insiemi A e B, l'insieme intersezione è l'insieme formato dagli ELEMENTI COMUNI ad A e a B.
Quindi l'insieme intersezione dell'insieme dei RETTANGOLI e dell'insieme dei ROMBI è l'insieme dei parallelogrammi tali che il parallelogramma ha 4 angoli congruenti e il parallelogramma ha 4 lati congruenti. E' evidente, allora, che l'insieme intersezione è l'insieme dei QUADRATI.
In simboli scriveremo:

l'insieme dei RETTANGOLI intersecato l'insieme dei ROMBI è uguale all'insieme dei parallelogrammi tali che il parallelogramma appartiene all'insieme dei rettangoli e il parallelogramma appartiene all'insieme dei rombi.
Tale insieme è uguale all'insieme dei QUADRATI.
Graficamente, avremo: