TRIANGOLI CIRCOSCRITTI
Nella lezione precedente abbiamo visto cosa si intende per POLIGONO CIRCOSCRITTO e abbiamo affermato che un poligono si dice circoscritto se TUTTI i suoi LATI sono TANGENTI ad una CIRCONFERENZA di centro O.
Inoltre abbiamo detto che un poligono si può CIRCOSCRIVERE ad una CIRCONFERENZA se le BISETTRICI dei suoi angoli si INCONTRANO TUTTE in un UNICO PUNTO che è anche il CENTRO DELLA CIRCONFERENZA.
Ora ipotizziamo che il poligono che vogliamo circoscrivere ad una circonferenza sia un TRIANGOLO. Dallo studio dei triangoli sappiamo che le BISETTRICI DEL TRIANGOLO si incontrano tutte in UNO STESSO PUNTO detto INCENTRO del triangolo.
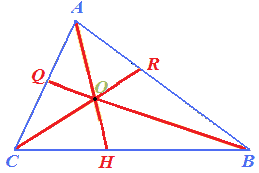
Essendo l'INCENTRO del triangolo unico è evidente che è SEMPRE POSSIBILE CIRCOSCRIVERE il triangolo ad una circonferenza:
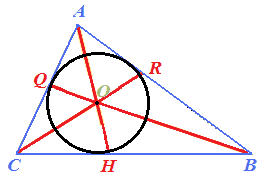
Osserviamo, le bisettrici di tutti gli angoli del triangolo si incontrano in un unico punto che è l'incentro del triangolo, ma anche il centro della circonferenza.
Quindi, possiamo dire che OGNI TRIANGOLO è un poligono CIRCOSCRITTIBILE.
Ricordiamo che qualsiasi triangolo noi disegniamo l'INCENTRO è sempre INTERNO al triangolo.






