RELAZIONE TRA I LATI DI UN POLIGONO
Immaginiamo di avere 5 segmenti lunghi rispettivamente:
AB = 8 cm
BC = 5 cm
CD = 4 cm
DE = 6 cm
EA = 3 cm
e di voler disegnare con essi un pentagono.
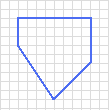
Come potete osservare abbiamo potuto disegnare tranquillamente il nostro poligono.
Ora immaginiamo altri 5 segmenti lunghi rispettivamente:
AB = 16 cm
BC = 2 cm
CD = 3 cm
DE = 5 cm
EA = 4 cm.
Proviamo a disegnare con essi un pentagono. Noteremo che, per quanto possiamo provare, non riusciremo a disegnare un pentagono, ma riusciremo a disegnare solamente una LINEA SPEZZATA APERTA.
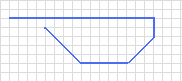
Facciamo un altro esempio. Supponiamo di avere i segmenti segmenti:
AB = 14 cm
BC = 3 cm
CD = 5 cm
DE = 3 cm
EA = 2 cm
e di voler disegnare con essi un pentagono. Noteremo che, anche questa volta, per quanto possiamo provare, non riusciremo a disegnare un pentagono, ma riusciremo a disegnare solamente una LINEA SPEZZATA APERTA.
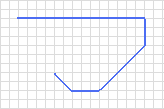
Chiediamoci, allora, perché nel primo caso siamo riusciti a disegnare un pentagono e negli altri due casi no.
Osserviamo con attenzione le misure dei segmenti nei tre casi proposti:
| 1° caso | 2° caso | 3° caso |
|---|---|---|
| 8 cm | 16 cm | 14 cm |
| 5 cm | 2 cm | 3 cm |
| 4 cm | 3 cm | 5 cm |
| 6 cm | 5 cm | 3 cm |
| 3 cm | 4 cm | 2 cm |
Notiamo che, nel primo caso ogni lato è sempre minore rispetto alla somma degli altri 4 lati. Infatti:
lato 8
somma degli altri 4 lati 5 + 4 + 6 + 3 =
18
confronto tra il lato e la somma degli altri 4 lati 8 < 18
lato 5
somma degli altri 4 lati 8 + 4 + 6 + 3 =
21
confronto tra il lato e la somma degli altri 4 lati 5 < 21
lato 4
somma degli altri 4 lati 8 + 5 + 6 + 3 =
22
confronto tra il lato e la somma degli altri 4 lati 4 < 22
lato 6
somma degli altri 4 lati 8 + 5 + 4 + 3 =
20
confronto tra il lato e la somma degli altri 4 lati 6 < 20
lato 3
somma degli altri 4 lati 8 + 5 + 4 + 6 =
23
confronto tra il lato e la somma degli altri 4 lati 3 < 23
Ora osserviamo, invece, ciò che accade nel secondo e nel terzo poligono confrontando ogni lato con la somma degli altri 4.
Secondo pentagono:
lato 16
somma degli altri 4 lati 2 + 3 + 5 + 4 =
14
confronto tra il lato e la somma degli altri 4 lati 16 > 14
lato 2
somma degli altri 4 lati 16 + 3 + 5 + 4
= 28
confronto tra il lato e la somma degli altri 4 lati 2 < 28
lato 3
somma degli altri 4 lati 16 + 2 + 5 + 4
= 27
confronto tra il lato e la somma degli altri 4 lati 3 < 27
lato 5
somma degli altri 4 lati 16 + 2 + 3 + 4
= 25
confronto tra il lato e la somma degli altri 4 lati 5
< 25
lato 4
somma degli altri 4 lati 16 + 2 + 3 + 5
= 26
confronto tra il lato e la somma degli altri 4 lati 4 < 26
Terzo pentagono:
lato 14
somma degli altri 4 lati somma degli altri 4 lati 3 + 5 + 3 + 2 =
13
confronto tra il lato e la somma degli altri 4 lati 14 > 13
lato 3
somma degli altri 4 lati 14 + 5 + 3 + 2
= 24
confronto tra il lato e la somma degli altri 4 lati 3 < 24
lato 5
somma degli altri 4 lati 14 + 3 + 3 + 2
= 22
confronto tra il lato e la somma degli altri 4 lati 5 < 22
lato 3
somma degli altri 4 lati 14 + 3 + 5 + 2
= 24
confronto tra il lato e la somma degli altri 4 lati 3 < 24
lato 2
somma degli altri 4 lati 14 + 3 +5 + 3 =
25
confronto tra il lato e la somma degli altri 4 lati 2< 25
Nel secondo e nel terzo pentagono vi è sempre un lato maggiore rispetto alla somma degli altri 4 lati.
Allora possiamo dire che affinché, dati alcuni segmenti, possiamo disegnare una linea spezzata semplice chiusa, è necessario che ogni segmento sia minore rispetto alla somma degli altri.
Da ciò ricaviamo la seguente regola:
in un qualsiasi POLIGONO, OGNI LATO è sempre MINORE rispetto alla SOMMA di TUTTI GLI ALTRI LATI.
Ovviamente, anche se noi abbiamo usato nei nostri esempi dei pentagoni, cioè poligoni con 5 lati, la regola vale per tutti i poligoni a prescindere dal numero dei loro lati.
Facciamo un'ultima osservazione.
Se dati alcuni segmenti volessimo disegnare con essi un poligono, non ci riusciremmo neppure nel caso in cui uno di essi fosse UGUALE alla somma di tutti gli altri. Quindi, ogni segmento deve essere MINORE rispetto alla somma di tutti gli altri.






