RECIPROCO DI UN NUMERO RELATIVO
- I numeri relativi
- Divisione di numeri relativi
- Potenze di numeri relativi con esponente negativo
- L'insieme dei numeri razionali relativi
Due numeri relativi si dicono RECIPROCI quando il loro PRODOTTO è UGUALE a +1.
Ovvero
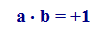
Quindi possiamo dire che il reciproco di a è quel numero b tale che moltiplicando il primo per il secondo abbiamo come risultato +1.
Il reciproco prende anche il nome di INVERSO o INVERSO MOLTIPLICATIVO.
Poiché per definizione il prodotto di due numeri
reciproci è positivo, necessariamente i due numeri devono avere lo
stesso segno: quindi, o sono entrambi positivi o entrambi negativi. Di
conseguenza si esclude lo zero quando si parla di reciproco.
SEGNO DEL NUMERO: +
SEGNO DEL RECIPROCO: +
SEGNO DEL NUMERO: -
SEGNO DEL RECIPROCO: -
LO
ZERO NON HA
RECIPROCO
Poiché moltiplicando un numero per il suo reciproco avremo come risultato +1, il reciproco di a sarà 1/a. Ovvero:
a
RECIPROCO:
1/a
Infatti:

Quindi per ottenere il reciproco di un numero dobbiamo dividere 1 per il numero stesso.
Esempio:
+5
RECIPROCO:
+1/5
-3
RECIPROCO: 1/(-3)
= -1/3
Per indicare il RECIPROCO di a possiamo scrivere:
1/a
oppure
(a)-1 (vedi anche Potenze di numeri relativi con esponente negativo)
+1 si dice AUTORECIPROCO, dato che il suo reciproco è se stesso.
Anche -1 si dice AUTORECIPROCO dato che il suo reciproco è se stesso.
Quindi:
+1
RECIPROCO:
1/(+1)=+1
-1
RECIPROCO:
1/(-1)=-1
+1
e -1 AUTORECIPROCI
Si chiamano NUMERI
RAZIONALI RELATIVI i NUMERI
RELATIVI il cui VALORE
ASSOLUTO è costituto da una FRAZIONE.
Esempi:
-1/2
+4/8
-12/5
NUMERI
RAZIONALI RELATIVI
Anche nel caso dei numeri razionali relativi si dicono RECIPROCI due numeri il cui PRODOTTO è UGUALE a + 1.
Il reciproco di un numero razionale relativo si ottiene SCAMBIANDO IL NUMERATORE COL DENOMINATORE.
Infatti:

Quindi per calcolare il reciproco di un numero razionale relativo dobbiamo SCAMBIARE IL NUMERATORE COL DEMINATORE.
Esempio:
+1/5
RECIPROCO:
+5/1 = +5
-3/4
RECIPROCO:
-4/3
+7/2
RECIPROCO:
+2/7
- Esercizio 47 - Potenze di numeri relativi
- Esercizio 48 - Potenze di numeri relativi
- Esercizio 49 - Potenze di numeri relativi






