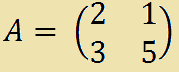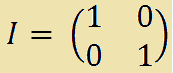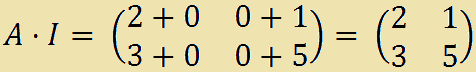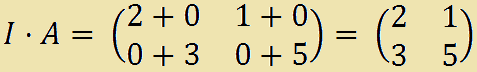MATRICE IDENTITA'
Si chiama MATRICE IDENTITA' o MATRICE UNITA' una matrice quadrata i cui ELEMENTI della DIAGONALE PRINCIPALE sono tutti uguali ad UNO, mentre i restanti elementi sono tutti uguali a ZERO.
Esempio:
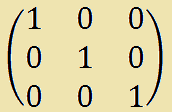
Quella che abbiamo appena scritto è una MATRICE IDENTITA'.
Per indicare la matrice identità si usa la LETTERA I MAIUSCOLA. Potremo scrivere, quindi:
I
oppure
In
che si legge
i con enne.
Il simbolo
In
si usa quando si vuole precisare l'ordine della matrice.
Ad esempio, la matrice che abbiamo scritto sopra è di ordine tre, quindi la indicheremo con
I3.
La POTENZA di una MATRICE IDENTITA' è sempre una MATRICE IDENTITA'.
Ovvero:
Im = I
con m intero e positivo.
Esempio.
Data la matrice
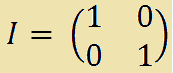
vogliamo calcolare I2.
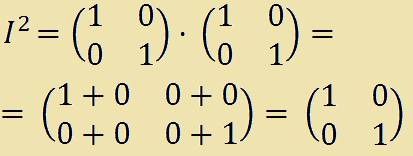
Osserviamo, inoltre, che la MATRICE IDENTITA' è l'ELEMENTO NEUTRO rispetto al prodotto di matrici. Ovvero, data la matrice A non nulla, avremo:
I · A = A · I = A.
Esempio: