FUNZIONE PARTE INTERA
Consideriamo la FUNZIONE f che associa a QUALUNQUE x appartenente ai REALI la PARTE INTERA di x.
Una funzione simile si scrive nel modo seguente:
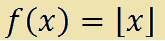
che si legge
f di x uguale alla parte intera di x.
Essa viene chiamata anche FUNZIONE PARTE INTERA.
Il GRAFICO DI QUESTA FUNZIONE risulta essere alquanto particolare.
Vediamo i valori che assume la parte intera di x al variare di x:
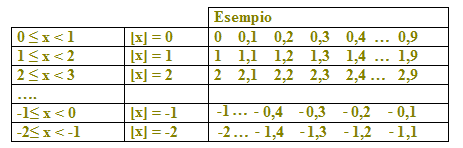
In altre parole:
- quando x assume valori compresi tra 0 e 1, con zero incluso, la parte intera di x è 0;
- quando x assume valori compresi tra 1 e 2, con uno incluso, la parte intera di x è 1;
- e così via.
Quindi possiamo dire che, se
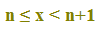
che si legge
x è compreso tra n ed n+1, con n incluso
la PARTE INTERA di x è uguale ad n.
Ora disegniamo il grafico di questa funzione:
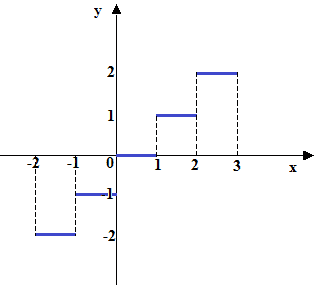
Una funzione di questo tipo prende il nome di FUNZIONE A SCALA o funzione A GRADINI dato l'aspetto che la funzione presenta.
Su alcuni testi per indicare la parte intera di x, viene usato il simbolo [x].






