DISTANZA DI UN PUNTO DA UNA RETTA
- Distanza di una retta dall'origine degli assi
- Distanza di una retta dall'origine degli assi: esercizi
- Traslazione degli assi cartesiani
Dopo aver visto, nella lezione precedente come possiamo calcolare la distanza di una retta dall'origine degli assi, ora ci poniamo come obiettivo quello di determinare la DISTANZA di una RETTA da un PUNTO.
Sia il punto
P0 ( x0 ; y0)
un generico punto.
Vogliamo sapere qual è la sua distanza dalla retta
ax + by + c = 0.
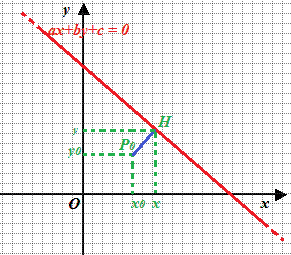
In altre parole si tratta di trovare la lunghezza del segmento P0H. Notiamo che le coordinate del punto H sono x e y.
Ora effettuiamo una TRASLAZIONE degli ASSI in modo da portare l'origine in P0:
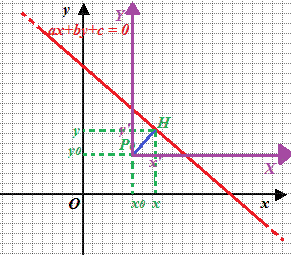
Le coordinate del punto H sul nuovo sistema di assi (quello indicato in viola) sono x' e y'.
La relazione che lega le coordinate del punto H sul sistema di assi avente O come origine (ed indicato in nero) e il sistema di assi avente come origine P0 (ed indicato in viola) è data da:
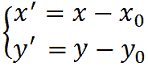
Da essa ricaviamo i valori di x e di y, ovvero:
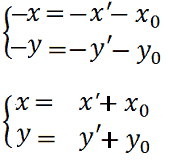
L'EQUAZIONE della RETTA nel nuovo sistema di assi aventi P0 come origine si ottiene sostituendo ad x e ad y i termini indicati nei secondi membri delle precedenti due equazioni:
ax + by + c = 0
a (x' + x0) + b (y' + y0) + c = 0
ax' + ax0 + by' + by0 + c = 0
ax' + by' + ax0 + by0 + c = 0.
In questa nuova equazione le nostre incognite sono ax' e by', mentre ax0 + by0 + c rappresentano il termine noto:
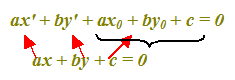
Noi sappiamo, dalla lezione precedente, che la DISTANZA di una retta dall'ORIGINE degli assi, è data dalla formula:
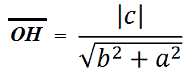
Applichiamo, dunque, questa formula per determinare la distanza della retta dall'origine P0. Ovviamente dovremo utilizzare, a tal fine, l'equazione della retta appena scritta e riferita al sistema di assi aventi P0 come origine.
Quindi avremo:
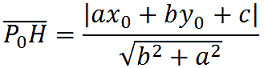
che ovviamente potrà essere scritta anche come:
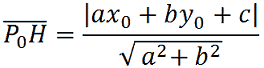
Vediamo un esempio di applicazione di tale formula.
Esempio:
determinare la distanza tra il punto P(-3; 2) e la retta di equazione
4x + 2y + 1 =0.
Nel nostro esempio abbiamo che:
>x0 = -3
y0 = 2
a = 4
b = 2
c = 1.
Quindi la formula diventa
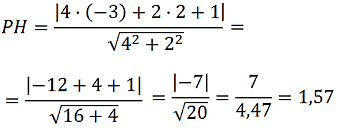
La distanza cercata è 1,57.






