FORMULA DI BISEZIONE DELLA TANGENTE
- Formule goniometriche
- Formula di duplicazione del seno
- Formula di bisezione del seno
- Formula di bisezione del coseno
- Formula di bisezione della tangente
- Seconda relazione fondamentale della goniometria
Nella lezione precedente abbiamo visto che la FORMULA DI BISEZIONE della TANGENTE è:
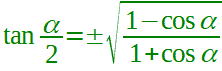
Abbiamo detto, però, sempre in quella lezione, che esistono altri due modi di esprimere la formula di bisezione della tangente: questi due modi, che vedremo in questa lezione, hanno il vantaggio di NON presentare il simbolo di RADICE ed il DOPPIO SEGNO.
Iniziamo col vedere la prima di queste due formule.
Dalla seconda relazione fondamentale della goniometria sappiamo che:
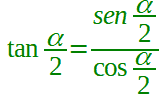
Ora moltiplichiamo numeratore e denominatore per 2 cos α/2
Per poter eseguire tale operazione dobbiamo porre come condizione che:
2 cos α/2 ≠ 0
che equivale a dire:
cos α/2 ≠ 0
Noi sappiamo che il coseno di un angolo è uguale a zero quando l'angolo misura 90°, 270° e così via. Quindi possiamo dire che la condizione da noi posta equivale a scrivere:
α/2 ≠ π/2 + kπ
che, moltiplicando primo e secondo membro per 2, diventa:
α ≠ π+ 2kπ
con k ∈ Z
Posta questa condizione torniamo alla nostra formula che, una volta eseguita la moltiplicazione, diventa:
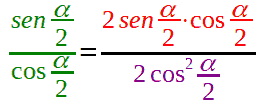
Ora osserviamo il numeratore e ricordiamo che la FORMULA di DUPLICAZIONE del SENO ci dice che:
sen 2 α = 2 sen α · cos α
Quindi, il nostro numeratore non è altro che il SENO dell'angolo doppio di α/2, cioè il SENO dell'angolo α. Quindi, la nostra formula diventa:
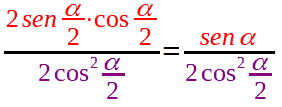
Passiamo al denominatore. Se andate a rileggere la lezione sulla FORMULA di BISEZIONE del COSENO vedrete che, prima di giungere alla formula definitiva di bisezione del coseno, avevamo visto che
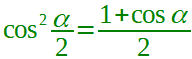
Sostituendo questa formula al denominatore della nostra frazione, avremo:
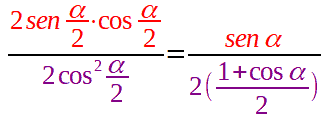
Semplifichiamo ed otteniamo:
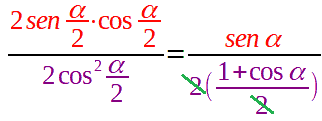
Quindi, un'altra FORMULA di BISEZIONE della TANGENTE è:
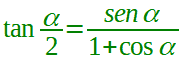
posto
α ≠ π+ 2kπ
con k ∈ Z
Passiamo all'altra formula.
Scriviamo sempre:
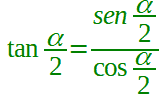
Ora moltiplichiamo numeratore e denominatore per 2 sen α/2
Per poter eseguire tale operazione dobbiamo porre come condizione che:
2 sen α/2 ≠ 0
che equivale a dire:
sen α/2 ≠ 0
Noi sappiamo che il seno di un angolo è uguale a zero quando l'angolo misura 0°, 180° e così via. Quindi possiamo dire che la condizione da noi posta equivale a scrivere:
α/2 ≠ kπ
che, moltiplicando primo e secondo membro per 2, diventa:
α ≠ 2kπ
con k ∈ Z
Posta questa condizione torniamo alla nostra formula che, una volta eseguita la moltiplicazione, diventa:
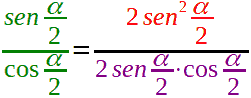
Ora osserviamo il numeratore della nostra frazione. Come abbiamo già detto prima, dalla FORMULA di BISEZIONE del SENO sappiamo che
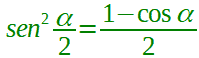
Sostituendo questa formula al numeratore della nostra frazione, avremo:
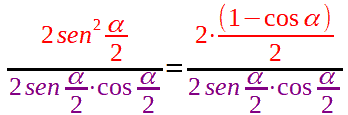
Ora passiamo ad esaminare il denominatore e ricordiamo che la FORMULA di DUPLICAZIONE del SENO ci dice che:
sen 2 α = 2 sen α · cos α
Quindi, il nostro denominatore non è altro che il SENO dell'angolo doppio di α/2, cioè il SENO dell'angolo α. Quindi, la nostra formula diventa:
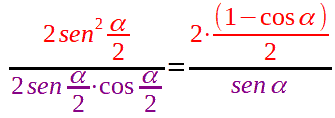
Semplifichiamo ed otteniamo:
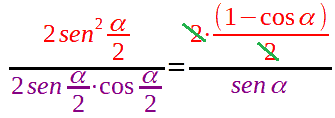
Quindi, un'altra FORMULA di BISEZIONE della TANGENTE è:
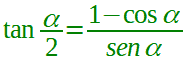
posto
α ≠ 2kπ
con k ∈ Z






