ARCHI DI UNA CIRCONFERENZA
- La circonferenza e il cerchio
- Parti di una circonferenza e di un cerchio
- Corde di una circonferenza
- Il segmento
Nella lezione precedente abbiamo visto che si chiama CORDA un SEGMENTO che UNISCE DUE PUNTI QUALSIASI di una CIRCONFERENZA.
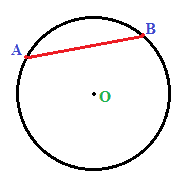
Nell'immagine sopra abbiamo scelto due punti qualsiasi della circonferenza: il punto A e il punto B: il segmento AB è una CORDA della CIRCONFERENZA.
In questo modo la nostra CIRCONFERENZA viene DIVISA in DUE PARTI, ognuna delle quali è detta ARCO. Nell'immagine sotto abbiamo evidenziato le due parti con due colori diversi: arancio la prima e viola la seconda.
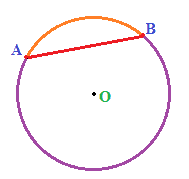
A e B sono gli ESTREMI dell'ARCO.
L'arco viene indicato con il seguente simbolo:

che si legge
arco AB.
Poiché A e B sono gli estremi di entrambi gli archi nei quali risulta divisa la circonferenza dalla corda, per evitare confusioni si nomina un ulteriore punto appartenente all'arco. Ad esempio:
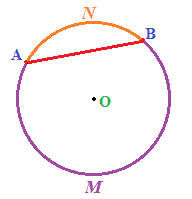
Per cui chiamiamo:

che si legge
arco ANB
il primo arco, che nel disegno sopra abbiamo indicato in arancio e

che si legge
arco AMB
il secondo arco, che nel disegno sopra abbiamo indicato in viola.
Oppure possiamo indicare i due archi in questo modo:
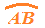
il primo arco, che nel disegno sopra abbiamo indicato in arancio e che rappresenta un ARCO CONVESSO, quello di minore lunghezza
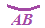
il secondo arco, che nel disegno sopra abbiamo indicato in viola e che rappresenta un ARCO CONCAVO, quello di maggiore lunghezza.
Quando non viene specificato il tipo di arco si intende quello convesso.
Inoltre si dice
che la CORDA AB
SOTTENDE l'arco .
.
Oppure possiamo dire che l'arco  è SOTTESO dalla CORDA AB.
è SOTTESO dalla CORDA AB.
In una stessa circonferenza ARCHI CONGRUENTI sottendono CORDE CONGRUENTI e viceversa.
In due circonferenze congruenti ARCHI CONGRUENTI sottendono CORDE CONGRUENTI e viceversa.
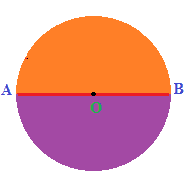
Se in una circonferenza disegniamo il DIAMETRO esso divide:
- la circonferenza
in DUE ARCHI CONGRUENTI
detti SEMICIRCONFERENZE
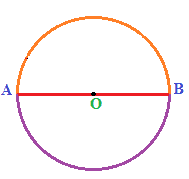
-
il cerchio
in DUE PARTI CONGRUENTI
dette SEMICERCHI