LE GRANDEZZE
Immaginiamo di avere un pezzo di stoffa. Ora possiamo immaginare un pezzo di stoffa che abbia una lunghezza doppia rispetto alla precedente.
Osserviamo un pezzo di terreno. Possiamo sempre trovare un pezzo di terreno che ha una estensione doppia rispetto al precedente.
In questi e in altri casi ci troviamo di fronte a delle GRANDEZZE: la LUNGHEZZA del pezzo di stoffa, la SUPERFICIE del pezzo di terreno.
L'espressione GRANDEZZA è genericamente utilizzata per indicare QUALCOSA che può essere RADDOPPIATO. Nei nostri esempi abbiamo parlato di lunghezza e di superficie, ma si potrà trattare anche di peso, capacità, di volume, di angoli, ecc..
Due lunghezze, due angoli, due superfici, si dicono GRANDEZZE OMOGENEE. Quindi, con l'espressione GRANDEZZE OMOGENEE intendiamo delle GRANDEZZE della STESSA SPECIE.
Due lunghezze sono tra loro confrontabili, lo stessa dicasi per due angoli, due segmenti, due superfici, ecc.. Quindi due GRANDEZZE OMOGENEE sono tra loro CONFRONTABILI.
Le GRANDEZZE OMOGENEE possono essere tra loro SOMMATE, in modo da ottenere una grandezza MULTIPLA rispetto a quella data.
Osserviamo il disegno riportato sotto.
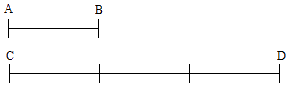
Abbiamo due segmenti:
- il segmento AB
- il segmento CD.
Il segmento CD è pari a 3 volte il segmento AB: quindi esso è MULTIPLO di AB.
Osserviamo, ora, un'altra immagine.
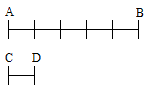
Il segmento AB può essere diviso in tante parti uguali. Ad esempio, dividiamo il segmento AB in cinque parti uguali e, chiamiamo ognuna di queste, CD.
Il segmento CD è SOTTOMULTIPLO del segmento AB.






