PROPRIETA' DELLA RETTA
Su un foglio di carta fissiamo un punto A:

Ora, aiutandoci con una riga, tracciamo alcune rette passanti per il punto A. Per rendere più chiaro il grafico indichiamo ogni retta con un colore diverso:
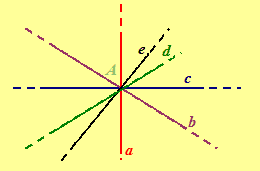
Una volta disegnate un bel po' di rette passanti per il punto A possiamo notare che è sempre possibile disegnarne ancora delle altre.
Possiamo dire allora che PER UN PUNTO PASSANO INFINITE RETTE.
Ora, invece, disegniamo due punti distinti A e B:

Ora proviamo a disegnare tutte le rette che passano sia per il punto A che per il punto B. Vedremo che è possibile disegnare un'unica retta passante per entrambi i punti:

Quindi possiamo affermare che PER DUE PUNTI PASSA UNA SOLA RETTA.
Per questa ragione si dice che DUE PUNTI DISTINTI A e B INDIVIDUANO una SOLA RETTA, la retta AB.
Di conseguenza, se due rette hanno due punti in comune, esse avranno anche tutti gli altri punti in comune:

In questo caso le due RETTE si dicono UGUALI.
Ne consegue che DUE RETTE DISTINTE non possono avere più di UN PUNTO IN COMUNE.
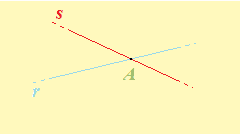
Quando due rette si incontrano in un punto si dice che esse sono INCIDENTI o SECANTI. Il punto comune ad entrambe le rette si dice INTERSEZIONE delle due rette.
Nel nostro esempio il punto A è l'intersezione delle rette r e s.






