ALTEZZA RELATIVA ALL'IPOTENUSA
Disegniamo il TRIANGOLO RETTANGOLO ABC:
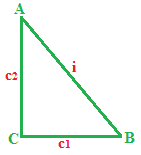
Nel triangolo abbiamo indicato con:
- i = l'ipotenusa;
- c1 = un cateto;
- c2 = l'altro cateto.
Ora noi sappiamo che l'AREA del TRIANGOLO RETTANGOLO si ottiene moltiplicando tra loro i due cateti e dividendo il prodotto per 2. cioè:
A = (c1 x c2)/2.
Da questa formula, otteniamo:
2 x A = c1 x c2.
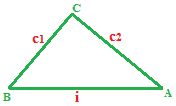
Proviamo ora a considerare come BASE del nostro triangolo l'IPOTENUSA:
Ora disegniamo l'ALTEZZA RELATIVA ALL'IPOTENUSA e la indichiamo con h:
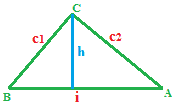
L'AREA del TRIANGOLO può essere ottenuta nel modo seguente:
A = (i x h)/2.
Da questa formula, otteniamo:
2 x A = i x h.
Quindi abbiamo detto che:
2 x A = c1 x c2
2 x A = i x h.
Di conseguenza, essendo l'area del triangolo sempre la stessa, e quindi anche il suo doppio prodotto, possiamo scrivere che:
c1 x c2 = i x h.
Ora DIVIDIAMO la doppia area per i e abbiamo
(c1 x c2)/ i = (i x h)/i.
Semplificando, dove è possibile, otteniamo:
(c1 x c2)/ i = h.
Abbiamo così trovato la misura di h, cioè dell'ALTEZZA RELATIVA ALL'IPOTENUSA.
In altre parole possiamo dire che la misura dell'ALTEZZA RELATIVA ALL'IPOTENUSA è data dal PRODOTTO delle misure dei due CATETI DIVISO l'IPOTENUSA.
Quindi:
h = (c1 x c2)/ i.
Nella prossima lezione vedremo alcune applicazioni di questa formula.






