CONFRONTO DI NUMERI RELATIVI
Iniziamo con il dire che due numeri relativi sono uguali se hanno lo stesso segno e lo stesso valore assoluto.
NUMERI
RELATIVI UGUALI
STESSO
SEGNO
STESSO
VALORE ASSOLUTO
Esempi:
+ 4 = + (2+2)
- 20 = - (5 + 15)
L'uguaglianza dei numeri relativi gode delle seguenti proprietà:
- a = a
PROPRIETA' RIFLESSIVA
- se a = b anche b = a
PROPRIETA' SIMMETRICA
- se a = b e b = c
anche a = c
PROPRIETA' TRANSITIVA
Da quanto abbiamo appena detto si deduce chiaramente che se due numeri relativi sono diversi o per segno, o per valore assoluto, essi non sono uguali e si dicono, più precisamente, diseguali.
Per indicare che due numeri sono diseguali si usa il
segno 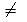
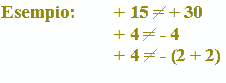
Vediamo ora come confrontare due numeri relativi.
Il primo modo che abbiamo per confrontare due numeri relativi e di rappresentarli su una retta.
Dati due numeri è sempre maggiore quello situato più a destra dell'altro.
Esempio:
+ 5 e - 3.
Li riportiamo su una retta.
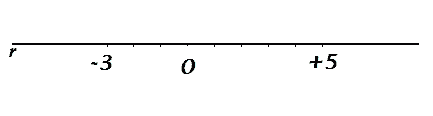
E evidente che +5 è situato più a destra rispetto a -3: quindi +5 è più grande di -3.
Cioè possiamo scrivere:
+ 5 > - 3.
Non volendo ricorrere alla rappresentazione grafica dobbiamo applicare la seguente regola:
- ogni NUMERO POSITIVO
è MAGGIORE di ogni NUMERO NEGATIVO
Esempio: + 5 > - 3
- di due NUMERI POSITIVI
è MAGGIORE quello che ha VALORE ASSOLUTO MAGGIORE
Esempio: + 10 e + 4
Valore assoluto di +10: 10
Valore assoluto di +4: 4
10 > 4
+10 > +4
- di due NUMERI
NEGATIVI è MAGGIORE quello che ha VALORE ASSOLUTO MINORE
Esempio: - 8 > - 6
Valore assoluto di - 8: 8
Valore assoluto di - 6: 6
6 < 8
- 6 > - 8
-
lo ZERO è MINORE di
ogni NUMERO POSITIVO e MAGGIORE di ogni
NUMERO NEGATIVO
Esempio: 0 < +4 0 > -15
Di conseguenza:
- se indichiamo con a un numero relativo positivo
possiamo scrivere che:
a > 0
- se indichiamo con a un numero relativo negativo possiamo scrivere che:
a < 0
- se indichiamo con a un numero relativo positivo
possiamo scrivere che:
- Esercizio 8 - Confronto di numeri relativi
- Esercizio 9 - Confronto di numeri relativi
- Esercizio 10 - Confronto di numeri relativi
- Esercizio 11 - Confronto di numeri relativi






