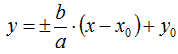FUOCHI, VERTICI ED ASINTOTI DELL'IPERBOLE TRASLATA
Dopo aver visto, nella lezione precedente, qual è l'EQUAZIONE dell'IPERBOLE TRASLATA, in questa lezione vedremo come, data l'equazione di una iperbole traslata, possiamo trovare le coordinate dei fuochi, dei vertici e l'equazione degli asintoti.
Esempio:
data l'iperbole di equazione
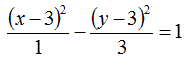
dire quali sono le coordinate del centro, dei vertici, dei fuochi e scrivere l'equazione degli asintoti.
Cominciamo col cercare le coordinate del centro P0. Noi sappiamo che l'EQUAZIONE DELL'IPERBOLE TRASLATA è del tipo:
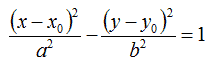
dove x0 e y0 rappresentano le coordinate del centro. Quindi, nel nostro caso abbiamo:
x0 = 3
y0 = 3.
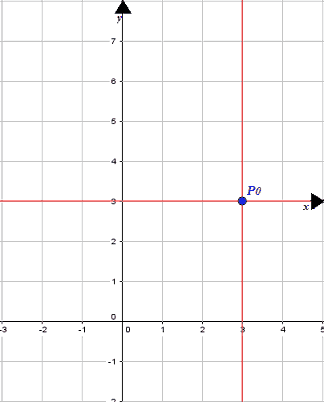
Pertanto le coordinate del centro sono:
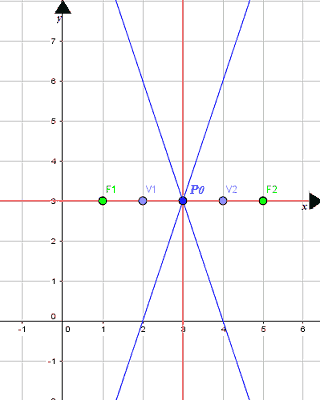
P0 (3; 3).
Disegniamo il centro della nostra iperbole e i suoi assi di simmetria.
Poiché la nostra equazione è
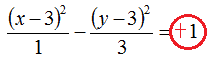
possiamo affermare che l'iperbole ha i suoi fuochi sull'asse parallelo a quello delle ascisse.
Quindi, iniziamo col trovare i suoi vertici.
Il SEMIASSE TRAVERSO è dato da
a = 1.
Tale valore rappresenta la distanza tra uno dei vertici e il centro dell'iperbole.
Iniziamo a cercare le coordinate dei vertici. Essi hanno sicuramente come ordinata 3.
Se il semiasse traverso è pari a 1, come abbiamo visto sopra, allora i vertici distano dal centro P0 di 1 a sinistra e a destra. In altre parole, le coordinate dei vertici saranno:
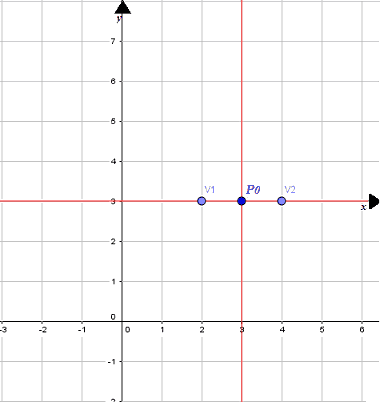
V1 (2; 3)
V2 (4; 3).
In altre parole le coordinate dei vertici si ottengono nel modo seguente:
V1 (x0 - a; y0)
V2 (x0 + a; y0).
Passiamo ai fuochi: anche essi hanno sicuramente come ordinata 3.
Iniziamo a trovarci il valore di c. Noi sappiamo che
b2 = c2 - a2.
Ovvero
3 = c2 - 1
-c2 = -3 - 1
c2 = 3 + 1 = 4
c = ±2.
Il valore di c rappresenta la semidistanza focale, cioè la distanza di ciascun fuoco dal centro P0. In altre parole, le coordinate dei fuochi saranno:
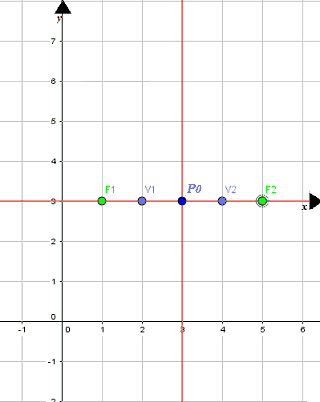
Quindi, le coordinate dei fuochi saranno:
F1 (1; 3)
F2 (5; 3).
In altre parole le coordinate dei fuochi si ottengono nel modo seguente:
F1 (x0 - c; y0)
F2 (x0 + c; y0).
Passiamo agli asintoti. Come sappiamo gli asintoti sono rette che passano per il centro di simmetria.
Se l'iperbole avesse avuto il centro nell'origine degli assi, gli asintoti avrebbero avuto come equazione:
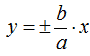
Come sappiamo b/a rappresenta l'inclinazione della retta. Questa rimane invariata pur essendo l'iperbole traslata. Quello che cambiano saranno i valori delle ascisse e delle ordinate, dovendosi effettuare la traslazione. Quindi avremo:
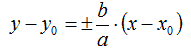
Da cui si ottiene
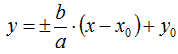
Nel nostro caso, quindi avremo:
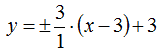
Da cui, prendendo il coefficiente angolare con segno positivo, si ha:
y = 3x - 9 + 3
y= 3x -6.
Mentre, prendendolo con segno negativo, si ha:
y = -3x + 9 + 3
y= -3x +12.
Disegniamo anche i due asintoti:
Concludiamo questa lezione dicendo che, se l'iperbole traslata, avesse avuto i fuochi sull'asse parallelo a quello delle ordinate, essa avrebbe avuto:
- i vertici
V1 (x0; y0 - b)
V2 (x0; y0 + b)
- i fuochi
F1 (x0; y0 - c)
V2 (x0; y0 + c)
-
gli asintoti
sempre uguali a