RETTA PASSANTE PER L'ORIGINE DEGLI ASSI
- Rappresentazione grafica di una funzione
- Diagramma della proporzionalità diretta
- Equazione della retta
- Costanti e variabili
Nella lezione precedente abbiamo visto che l'EQUAZIONE di una RETTA passante per L'ORIGINE degli ASSI è la seguente:
y = m · x
con m che è una COSTANTE.
Proviamo ora ad assegnare ad m dei valori diversi.
Cominciamo con il porre
m = 1.
La nostra equazione diventa:
y = 1 · x
y = x.
Costruiamo la nostra tabella e disegniamo l'equazione:
| x | y |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
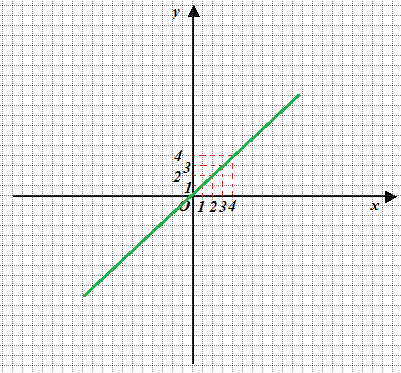
Ora poniamo
m = 1/2.
La nostra equazione diventa:
y = x/2
Costruiamo la nostra tabella e disegniamo l'equazione:
| x | y |
|---|---|
| 1 | 1/2 |
| 2 | 1 |
| 3 | 3/2 |
| 4 | 2 |
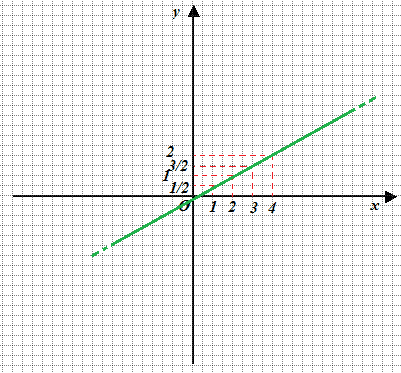
Ora poniamo
m = 3.
La nostra equazione diventa:
y = 3 · x.
Costruiamo la nostra tabella e disegniamo l'equazione:
| x | y |
|---|---|
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
| 4 | 12 |
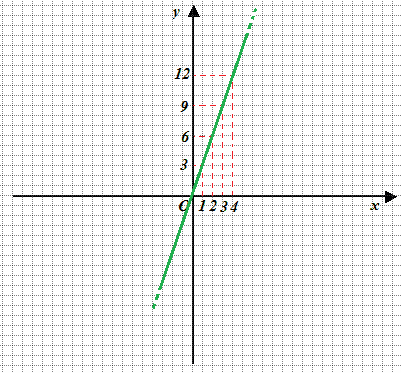
Ora facciamo due considerazioni.
La prima: esattamente come avevamo affermato ognuna di quelle che abbiamo disegnato è una RETTA passante per l'ORIGINE degli assi.
La seconda: notiamo che, al variare della costante m, varia l'INCLINAZIONE della RETTA rispetto all'asse delle ascisse. Per questa ragione, la m, si dice COEFFICIENTE ANGOLARE della retta.
Infine facciamo un'osservazione pratica, dato che per due punti passa una retta e una soltanto, per disegnare una retta sugli assi cartesiani è sufficiente individuare solamente due punti per i quali essa passa.
Esempio:
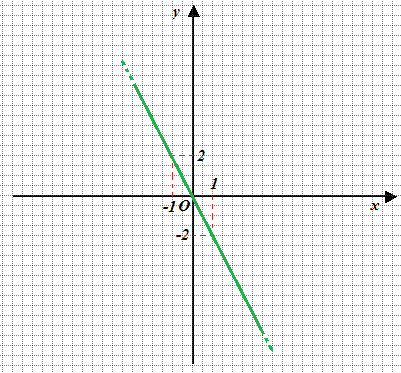
disegnare la retta di equazione
y = -2x.
Costruiamo la nostra tabella limitandoci ad individuare due soli punti:
| x | y |
|---|---|
| 1 | -2 |
| -1 | +2 |
Disegniamo i due punti e la retta: