ESERCIZI SULLE DISEQUAZIONI DI PRIMO GRADO
Esercizio 6
Risolvere la seguente disequazione:
- 10x + 5 ≥ - 4x + 9x.
Svolgimento
Portiamo a primo membro -4x e +9x cambiando il segno di entrambi e portiamo a secondo membro +5, cambiandogli di segno. In questo modo avremo a primo membro tutte le incognite e a secondo membro i termini noti:
- 10x + 4x – 9x ≥ - 5.
Ora riduciamo i termini simili, cioè facciamo la somma algebrica di -10x, +4x, -9x.
Avremo:
- 15x ≥ -5.
Poiché il coefficiente della x è negativo è necessario cambiargli di segno moltiplicando per -1 entrambi i termini della disequazione. In questo caso occorre ricordare che è necessario cambiare il verso della disequazione.
Quindi avremo:
15x ≤ 5.
Ora dividiamo entrambi i termini della disequazione per il coefficiente della x, ovvero per 15. Quindi avremo:
x ≤ 5/15.
Semplifichiamo ed otteniamo:
x ≤ 1/3.
Vediamo, ora, come possiamo rappresentare il risultato ottenuto. Riportiamo, i vari metodi possibili:
x ≤ 1/3
oppure
{x ∈ R : x ≤ 1/3}
oppure
] -∞ ; 1/3]
oppure
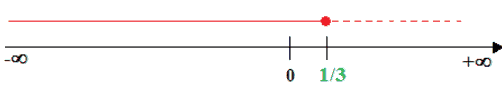
In questo caso la linea continua indica che la disequazione è verificata per i valori di x inferiori ad 1/3.
Il pallino pieno in corrispondenza di 1/3 indica che tale valore è compreso tra quelli che soddisfano la disequazione.
- Esercizio 1 - Esercizio sulle disequazione di primo grado intere
- Esercizio 2- Esercizio sulle disequazione di primo grado intere
- Esercizio 3 - Esercizio sulle disequazione di primo grado intere
- Esercizio 4 - Esercizio sulle disequazione di primo grado intere
- Esercizio 5 - Esercizio sulle disequazione di primo grado intere
- Esercizio 7 - Esercizio sulle disequazione di primo grado intere
- Esercizio 8 - Esercizio sulle disequazione di primo grado intere
- Esercizio 9 - Esercizio sulle disequazione di primo grado intere
- Esercizio 10 - Esercizio sulle disequazione di primo grado intere
- Esercizio 11 - Esercizio sulle disequazione di primo grado intere
- Esercizio 12 - Esercizio sulle disequazione di primo grado intere
- Esercizio 13 - Esercizio sulle disequazione di primo grado intere
- Esercizio 14 - Esercizio sulle disequazione di primo grado intere
- Esercizio 15 - Esercizio sulle disequazione di primo grado intere
- Esercizio 16 - Esercizio sulle disequazione di primo grado intere
- Esercizio 17 - Esercizio sulle disequazione di primo grado intere
- Esercizio 18 - Esercizio sulle disequazione di primo grado intere






