CIRCOCENTRO
- Triangoli
- Elementi del triangolo
- Triangolo rettangolo
- Elementi e punti notevoli di un triangolo
- Assi dei lati di un triangolo
- Figure geometriche equivalenti e figure geometriche congruenti
Nella lezione precedente abbiamo visto che l'ASSE di un TRIANGOLO relativo ad un lato è la RETTA ad ESSO PERPENDICOLARE passante per il PUNTO MEDIO del lato considerato.
Inoltre abbiamo osservato che gli assi del triangolo si incontrano tutti in UNO STESSO PUNTO detto CIRCOCENTRO DEL TRIANGOLO che abbiamo indicato con la lettera O:
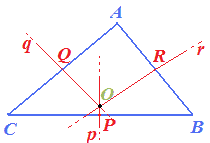
Il triangolo che abbiamo disegnato è un TRIANGOLO ACUTANGOLO: in questo caso il CIRCOCENTRO è INTERNO al triangolo.
Vediamo cosa accade se disegniamo un TRIANGOLO RETTANGOLO o un TRIANGOLO OTTUSANGOLO.
Partiamo dal TRIANGOLO RETTANGOLO:
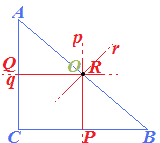
Come si può notare il CIRCOCENTRO coincide con il PUNTO MEDIO DELL'IPOTENUSA.
Disegniamo ora un TRIANGOLO OTTUSANGOLO, i suoi assi e il suo circocentro:
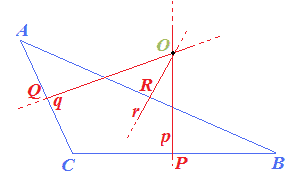
Come si può notare il CIRCOCENTRO è un PUNTO ESTERNO al triangolo.
Quindi, ricapitolando, il CIRCOCENTRO:
- nel TRIANGOLO ACUTANGOLO è un punto INTERNO al triangolo;
- nel TRIANGOLO RETTANGOLO coincide con il PUNTO MEDIO DELL'IPOTENUSA;
- nel TRIANGOLO OTTUSANGOLO è un punto ESTERNO al triangolo.
Ora torniamo ad osservare il nostro triangolo acutangolo:

Disegniamo con delle linee verdi la DISTANZA del CIRCOCENTRO O dai tre vertici A, B, C. Avremo:
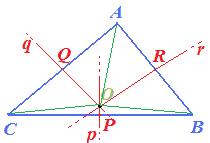
I segmenti AO, OB e OC hanno tutti la STESSA LUNGHEZZA. Possiamo, quindi scrivere che
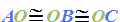
che si legge
AO è congruente ad OB che è congruente ad OC.
Qualsiasi triangolo noi disegniamo il suo CIRCOCENTRO è sempre EQUIDISTANTE dai VERTICI.






