SIMMETRIA CENTRALE
Dato il piano α (che si legge alfa), fissiamo un punto O e un punto P qualsiasi.
Ora disegniamo la retta r che unisce i due punti.
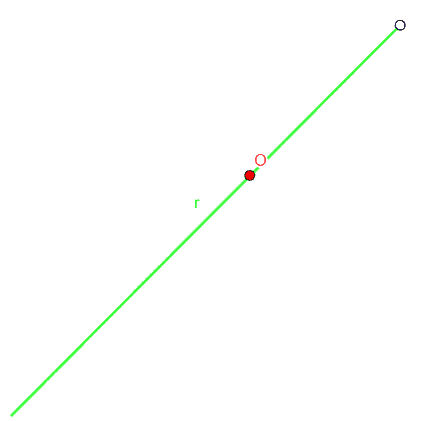
Misuriamo la distanza OP e segniamo, sempre sulla retta r, il punto P' tale che:
- esso sia situato dalla PARTE OPPOSTA di P rispetto ad O;
- e che la DISTANZA OP sia uguale alla distanza OP'.
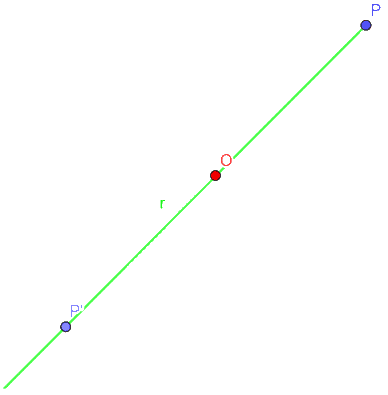
I punti P e P' si dicono SIMMETRICI rispetto al punto O.
Chiaramente, essendo la distanza PO uguale alla distanza OP', O rappresenta il PUNTO MEDIO del segmento PP'.
Andiamo ora a disegnare una figura piana F.
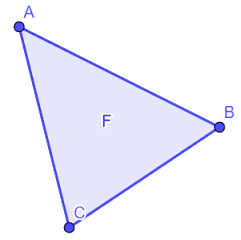
Disegniamo un punto qualsiasi che chiamiamo O.
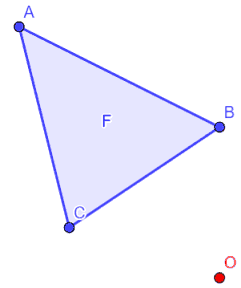
Uniamo i punti B ed O con una retta ed andiamo a disegnare il punto B' tale che:
- esso sia situato dalla PARTE OPPOSTA di B rispetto ad O;
- e che la DISTANZA OB sia uguale alla distanza OB'.
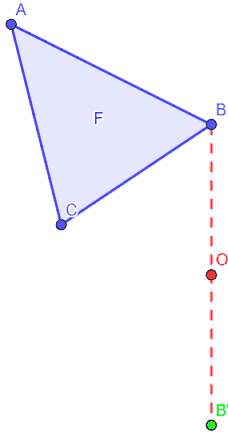
Ripetiamo questa costruizione per tutti i vertici della figura F in modo da costruire la figura F' .
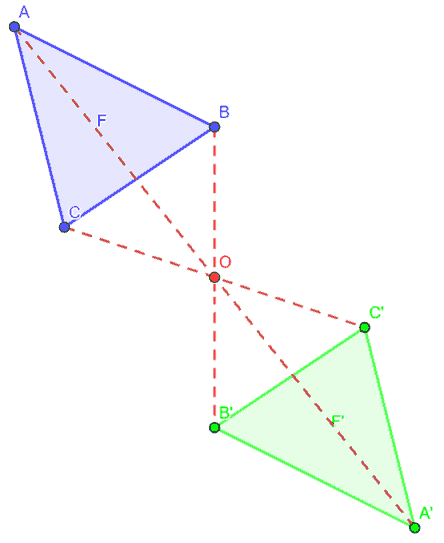
Tra i punti delle due figure si crea una CORRISPONDENZA BIUNIVOCA dato che ad ogni punto della figura F corrisponde un solo punto della figura F' e viceversa.
Questa corrispondenza prende il nome di SIMMETRIA CENTRALE avente per CENTRO il punto O e la si indica con il simbolo SO che si legge, appunto "Simmetria centrale di centro O".
I punti A ed A',
B e B',
C e C', si dicono
OMOLOGHI o CORRISPONDENTI nella simmetria centrale
SO.
Ora prendiamo un foglio di carta trasparente, ricalchiamo il triangolo F e sovrapponiamolo al triangolo F': vedremo che i due triangoli sono perfettamente sovrapponibili. Quindi possiamo dire che le due figure sono CONGRUENTI.
Adesso andiamo a fissare sul piano un punto A e un punto O qualsiasi.

E disegniamo il punto A' simmetrico di A rispetto al punto O.

Ora fissiamo un punto B qualsiasi.
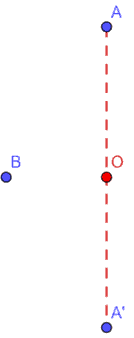
E disegniamo il punto B' simmetrico di B rispetto al punto O.
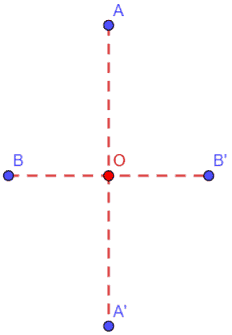
Costruiamo la figura AB'A'B.
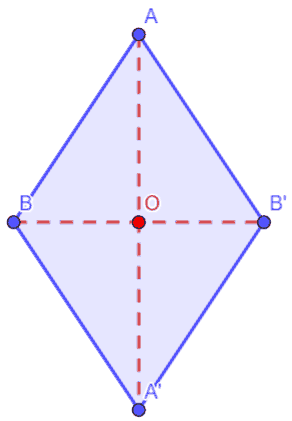
Il punto O prende il nome di CENTRO DI SIMMETRIA della figura AB'A'B.
Possiamo dire, quindi, che se TUTTI i PUNTI di una FIGURA sono SIMMETRICI A DUE A DUE rispetto ad un punto O si dice che questo punto è un CENTRO DI SIMMETRIA per quella figura.
Nella prossima lezione continueremo a parlare di simmetrie centrali occupandoci del rapporto tra simmetria centrale e rotazione.






