PROIEZIONE ORTOGONALE DI UN SEGMENTO SU UNA RETTA
Abbiamo visto, in una precedente lezione che nel disegno che segue

il punto B si chiama:
- PIEDE DELLA PERPENDICOLARE condotta da A alla retta r;
- PROIEZIONE di A su r.
Ora disegniamo:
- una RETTA r
- un SEGMENTO AB che NON APPARTENGA ad r.
Avremo:

Ora disegniamo la PERPENDICOLARE alla retta r PASSANTE per il punto A:

E chiamiamo con A' la PROIEZIONE di A sulla retta r:

A questo punto disegniamo la PERPENDICOLARE alla retta r PASSANTE per il punto B e chiamiamo con B' la PROIEZIONE di B sulla retta r:

Abbiamo così individuato, sulla retta r, un segmento denominato A'B':
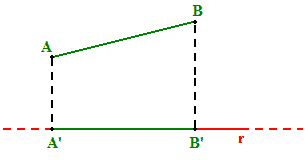
Il segmento A'B' prende il nome di PROIEZIONE ORTOGONALE del segmento AB sulla retta r.
Possiamo allora affermare che, si chiama PROIEZIONE ORTOGONALE di un SEGMENTO su una retta, il SEGMENTO APPARTENENTE ALLA RETTA e COMPRESO fra le PROIEZIONI DEGLI ESTREMI DEL SEGMENTO dato sulla retta.






