AREA DELLA CORONA CIRCOLARE
Disegniamo DUE CIRCONFERENZE CONCENTRICHE, cioè aventi lo stesso centro:
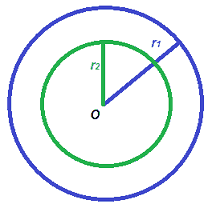
La prima circonferenza, disegnata in azzurro ha raggio r1.
La seconda circonferenza, disegnata in verde ha raggio r2.
Chiamiamo CORONA CIRCOLARE la PARTE di PIANO LIMITATA dalle due CIRCONFERENZE che nell'immagine sottostante abbiamo colorato in giallo ed indicato con la lettera A:
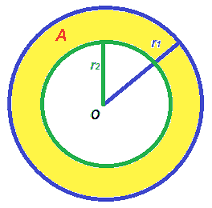
Ora vogliamo calcolare l'AREA della CORONA CIRCOLARE: è evidente che essa si ottiene come DIFFERENZA tra l'AREA DEL CERCHIO MAGGIORE di raggio r1 (che nella formula seguente abbiamo indicato come A) e l'AREA DEL CERCHIO MINORE di raggio r2 (che nella formula seguente abbiamo indicato come A). Cioè:
A - A = (π x r12)- (π x r22).
La stessa formula può essere scritta anche nel modo seguente
A π x (r12- r22).
In altre parole l'AREA della CORONA CIRCOLARE si ottiene MOLTIPLICANDO per la DIFFERENZA dei QUADRATI delle misure dei RAGGI delle due circonferenze che la limitano.
Esempio 1:
calcolare l'area della corona circolare limitata da due circonferenze che hanno i rispettivi raggio di cm 8 e cm 6.
Andiamo ad applicare la formula appena vista
A π x (r12- r22) =
= 3,14 x (82 - 62) =
= 3,14 x (64 - 36) =
= 3,14 x 28 = 87,92 cm2.
Esempio 2:
una corona circolare è limitata da due circonferenze lunghe rispettivamente cm 50,24 e cm 31,40. Calcolare la sua area.
In questo caso non conosciamo i raggi delle due circonferenze, quindi non possiamo applicare la formula appena vista. Sappiamo, però, quanto sono lunghe le due circonferenze e, pertanto, possiamo trovare i rispettivi raggi.
Avremo:
r1 = C/ 2 π = 50,24/ 6,28 = 8 cm
r2 = C/ 2 π = 31,40/ 6,28 = 5 cm
Ora possiamo applicare la formula per il calcolo dell'area della corona circolare
A π x (r12 - r22) =
= 3,14 x (82 - 52) =
= 3,14 x (64 - 25) =
= 3,14 x 39 = 122,46 cm2.






