METODI DI DIMOSTRAZIONE
- Proposizione matematica
- Implicazione logica
- Equivalenza logica
- Ipotesi e tesi
- Assiomi
- Tatutologie e contraddizioni
In una precedente lezione abbiamo visto che, quando l'IMPLICAZIONE
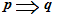
è VERA
si dice anche che essa è una PROPRIETA' o un TEOREMA.
Un TEOREMA è una PROPOSIZIONE che, partendo da delle condizioni iniziali giunge, attraverso una DIMOSTRAZIONE, a delle conclusioni.
Nel TEOREMA:
- p è la condizione dalla quale si parte e prende il nome di IPOTESI;
- q è la conclusione alla quale si giunge e prende il nome di TESI.
Ora vogliamo soffermarci sulla DIMOSTRAZIONE cioè su quelle considerazioni logiche che dobbiamo effettuare per poter dire che, essendo vera l'ipotesi è vera anche la tesi.
Due sono i METODI DI DIMOSTRAZIONE:
- metodo DIRETTO;
- metodo INDIRETTO.
METODO DIRETTO.
Il METODO DIRETTO è il metodo di dimostrazione più semplice. Partendo dall'ipotesi e utilizzando gli assiomi e le altre proprietà già dimostrate, attraverso una serie di deduzioni logiche, si giunge a poter dire che anche la tesi è vera.
METODO INDIRETTO.
Il METODO INDIRETTO viene anche detto DIMOSTRAZIONE PER ASSURDO. Per dimostrare che la tesi è vera, si suppone che sia vera la sua negazione e si perviene ad una contraddizione, cioè ad una proposizione che è sempre falsa.






