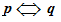CONDIZIONE NECESSARIA E SUFFICIENTE
Torniamo ad esaminare l'IMPLICAZIONE LOGICA vista nella undicesima lezione, ovvero:
p = Giovanni è abruzzese
q = Giovanni è italiano.
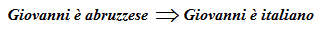
E' evidente che poiché Giovanni è abruzzese egli è certamente anche italiano. Quindi possiamo dire che l'essere Giovanni abruzzese è CONDIZIONE SUFFICIENTE perché egli sia anche italiano.
Al
tempo stesso il fatto che Giovanni è italiano è CONDIZIONE
NECESSARIA perché egli sia anche
abruzzese. Infatti, se Giovanni non fosse italiano non potrebbe essere
neppure abruzzese.
Quindi se
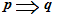
è
VERA
possiamo dire che:
p è CONDIZIONE SUFFICIENTE per q
(il fatto che Giovanni sia abruzzese è sufficiente per essere italiano)
q è CONDIZIONE NECESSARIA per p
(il
fatto che Giovanni sia italiano è necessario per essere abruzzese - se
Giovanni non fosse italiano non potrebbe essere neppure abruzzese)
In ogni TEOREMA:
- la verità dell'IPOTESI (p) è CONDIZIONE SUFFICIENTE per la verità della TESI (q);
- la verità della TESI (q) è CONDIZIONE NECESSARIA per la verità dell'IPOTESI (p).
Ora esaminiamo l'EQUIVALENZA LOGICA:
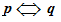
Come sappiamo essa equivale a dire che:
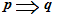
e
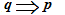
Quindi possiamo dire che:
- poiché p
implica q:
- p è CONDIZIONE SUFFICIENTE per q;
- q è CONDIZIONE NECESSARIA per p.
- poiché q
implica p:
- q è CONDIZIONE SUFFICIENTE per p;
- p è CONDIZIONE NECESSARIA per q.
Pertanto, ognuna della proposizioni p e q, è CONDIZIONE NECESSARIA e SUFFICIENTE per l'altra.
Il che viene espresso dicendo che
p è vera se, e solo se, q è vera.
Ad esempio:
p = T è un triangolo con tre lati uguali
q = T è un triangolo con tre angoli uguali.
T è un triangolo con
tre lati uguali se, e solo se, T é un triangolo con tre angoli uguali (e
viceversa).
Data la proprietà
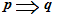
se scambiando l'ipotesi con la tesi è vera anche la proprietà
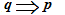
quest'ultima si chiama PROPRIETA' INVERSA di
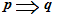
In questo caso le due proprietà possono essere riunite nell'unica proprietà: