DISEQUAZIONI GONIOMETRICHE ELEMENTARI NELLA COTANGENTE
Tra le DISEQUAZIONI GONIOMETRICHE ELEMENTARI troviamo quelle nella COTANGENTE che si presentano in uno dei modi che seguno:
cotg x < d
cotg x > d
cotg x ≤ d
cotg x ≥ d
con d ∈ R
che si legge
con d appartenente all'insieme dei numeri reali.
Per prima cosa poniamo le CONDIZIONI DI ESISTENZA: la funzione cotangente non è definita quando l'angolo assume valore 0 e quando assume valore π. Inoltre, poiché la funzione cotangente ha una periodicità di π, dobbiamo escludere dalle soluzioni le
x = kπ
(che include anche lo zero: infatti se k = 0 avremo che x = 0).
Quindi questi valori devono essere esclusi dalle possibili soluzioni della disequazione.
Per risolvere questo tipo di disequazioni usiamo il GRAFICO DELLA FUNZIONE GONIOMETRICA. Potremmo usare anche il metodo dell'angolo goniometrico, ma esso risulta più complesso.
Vediamo come procedere. Ipotizziamo di voler risolvere la disequazione:
cotg x < 1
Partiamo dal GRAFICO DELLA FUNZIONE COTANGENTE nell'intervallo [0, π] (entrambi gli estremi sono compresi nell'intervallo) dato che la funzione contangente ha periodo π e, quindi, una volta studiato questo intervallo possiamo estendere i risultati ottenuti a tutto l'asse reale.
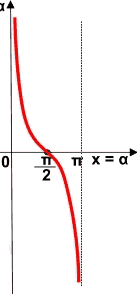
Sullo stesso grafico disegniamo la retta y = 1
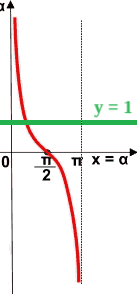
Ora individuiamo, sul grafico, i punti nei quali la funzione cotangente assume valori inferiori ad 1. Tali punti sono indicati nel grafico in blu:
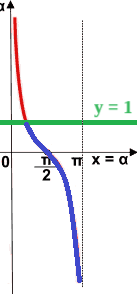
Notiamo che la cotangente assume valori inferiori ad 1 quando l'angolo è compreso tra π/4 e π.
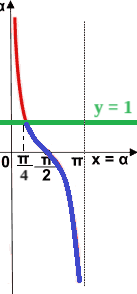
Poiché la funzione cotangente si ripete sempre allo stesso modo dopo un periodo di π, la nostra soluzione diventa:
π/4 + kπ < x < π + kπ
La soluzione trovata soddisfa le condizioni di esistenza poste e dunque è ammissibile.
Ovviamente, avremmo potuto scrivere la soluzione anche nel modo seguente:
]π/4 + kπ ; π + kπ[
entrambe le parentesi sono aperte, ad indicare che nessuna delle due soluzioni è compresa tra i risultati della disequazione.






