DISEQUAZIONI GONIOMETRICHE ELEMENTARI NELLA TANGENTE
Dopo aver visto come si risolvono le disequazioni goniometriche elementari nel seno e nel coseno, in questa lezione ci occuperemo delle disequazioni goniometriche elementari nella TANGENTE.
Queste disequazioni si possono presentare in uno dei modi seguenti:
tan x < c
tan x > c
tan x ≤ c
tan x ≥ c
con c ∈ R
che si legge
con c appartenente all'insieme dei numeri reali.
Come sempre andiamo a porre le nostre CONDIZIONI DI ESISTENZA: la funzione tangente non è definita quando
x = π/2
E, tenenuto conto che la periodicità della funzione tangente è π, i risultati che otterremo dalla soluzione della disequazione devono essere diversi da π/2 + kπ.
Anche per risolvere le disequazioni goniometriche elementari nella tangente possono essere usati i due metodi visti nelle lezioni precedenti, tuttavia il metodo della circonferenza goniometrica risulta piuttosto complesso da applicare, per questo lo tralascieremo dando la preferenza al metodo della RISOLUZIONE MEDIANTE IL GRAFICO DELLA FUNZIONE GONIOMETRICA.
Supponiamo di voler risolvere la disequazione:
tan x ≥ 1
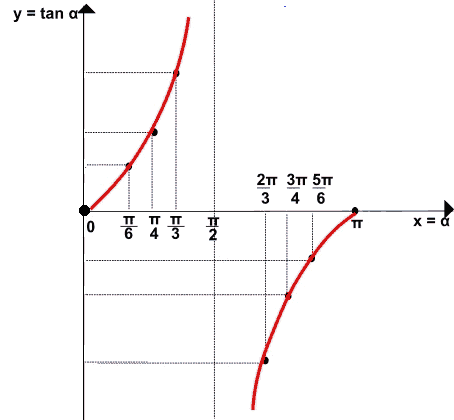
Partiamo dal GRAFICO DELLA FUNZIONE TANGENTE nell'intervallo [0, 2π[ (l'estremo 0 è compreso nell'intervallo, mentre l'estremo 2π è escluso dato che coincide con l'angolo 0)
Sullo stesso grafico disegniamo la retta y = 1
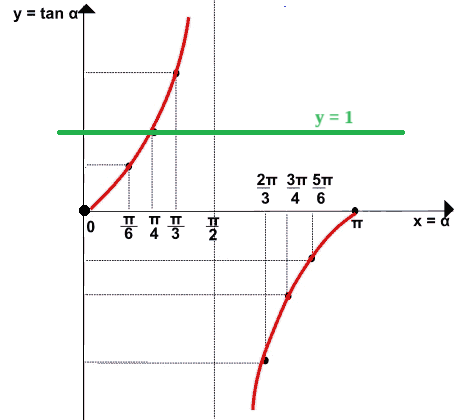
Osservando il grafico notiamo che la tangente di x risulta essere uguale o maggiore di 1 quando l'angolo è maggiore di π/4. Questo, fino a quando l'angolo non supera π/2. Infatti, una volta superato l'angolo π/2 la tangente diventa negativa, come si può vedere dall'immagine sottostante:
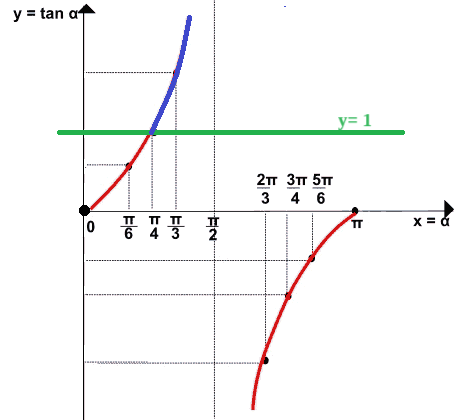
Di coseguenza la soluzione della nostra disequazione è
π/4 ≤ x < π/2
Notiamo che π/4 è compreso nelle soluzioni in quanto la tangente di tale angolo è pari ad 1 e noi stiamo cercando i valori di x tali che la sua tangente non sia solamente maggiore di 1, ma anche uguale ad 1. Invece, π/2 è escluso dalle soluzioni perché, come abbiamo detto in precedenza, quando l'angolo assume tale valore la tangente non è definita.
Poiché la funzione tangente si ripete sempre allo stesso modo dopo un periodo di π, la nostra soluzione diventa:
π/4 + kπ ≤ x < π/2 + kπ
Ovviamente, avremmo potuto scrivere la soluzione anche nel modo seguente:
[π/4 + kπ ; π/2 + kπ[
La prima parentesi è chiusa, ad indicare che π/4 è compreso nelle soluzioni, mentre la seconda parentesi è aperta ad indicare che π/2 non è compreso tra i risultati.






