TEOREMA SUGLI ANGOLI OPPOSTI AL VERTICE
- Gli angoli
- Angoli opposti al vertice
- Angolo piatto, angolo giro e angolo nullo
- Angolo consecutivi e angoli adiacenti
Sappiamo che due ANGOLI si dicono OPPOSTI AL VERTICE se i LATI DELL'UNO sono i PROLUNGAMENTI dei lati dell'altro.
Il TEOREMA sugli ANGOLI OPPOSTI AL VERTICE afferma che due ANGOLI OPPOSTI AL VERTICE sono UGUALI.
Vogliamo ora dimostrare questo teorema.
Disegniamo due angoli opposti al vertice:
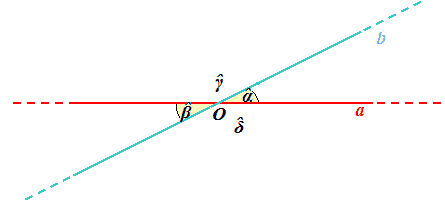
Abbiamo chiamato gli angoli formati dalle due rette rispettivamente:
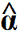- che si legge alfa;
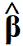- che si legge beta;
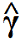- che si legge gamma;
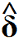- che si legge delta;
Noi vogliamo dimostrare che l'angolo α e l'angolo β, che sono OPPOSTI AL VERTICE, sono uguali tra loro.
Osserviamo che:
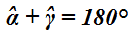
Infatti, i due angoli sono ADIACENTI e formano un ANGOLO PIATTO, e come sappiamo l'angolo piatto misura 180°.
Allo stesso modo possiamo scrivere che:
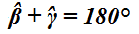
Essendo anch'essi due angoli adiacenti che formano un angolo piatto.
Quindi possiamo scrivere:
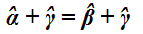
Ora sottraiamo, dal primo e dal secondo membro l'angolo γ, e avremo:
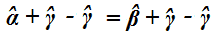
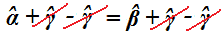
da cui:
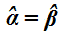
Abbiamo così dimostrato che l'angolo alfa e l'angolo beta, che sono due ANGOLI OPPOSTI AL VERTICE, sono UGUALI.
