PROPRIETA' DELLE OPERAZIONI CON LE PROPOSIZIONI: DIMOSTRAZIONE

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• Proposizione matematica
• Operazioni con le proposizioni
• Proprietà delle operazioni con le proposizioni
• Tavole della verità
• Disgiunzione o somma logica
• Congiunzione o prodotto logico

In una precedente lezione abbiamo visto quali sono le PROPRIETA' DELLE OPERAZIONI CON LE PROPOSIZIONI.

Ora vogliamo fornire una DIMOSTRAZIONE di tali proprietà. Per farlo ci avvaliamo delle TAVOLE DI VERITA'.

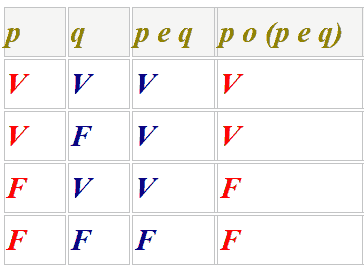
PROPRIETA' DELL'IDEMPOTENZA DELLA SOMMA LOGICA:

PROPRIETA' DELL'IDEMPOTENZA DEL PRODOTTO LOGICO:

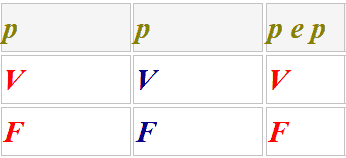
PROPRIETA' COMMUTATIVA DELLA SOMMA LOGICA:

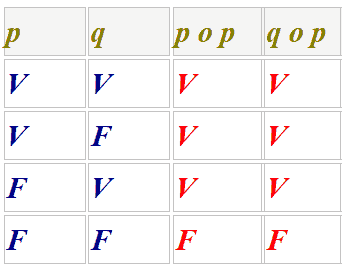
PROPRIETA' COMMUTATIVA DEL PRODOTTO LOGICO:

PROPRIETA' ASSOCIATIVA DELLA SOMMA LOGICA:

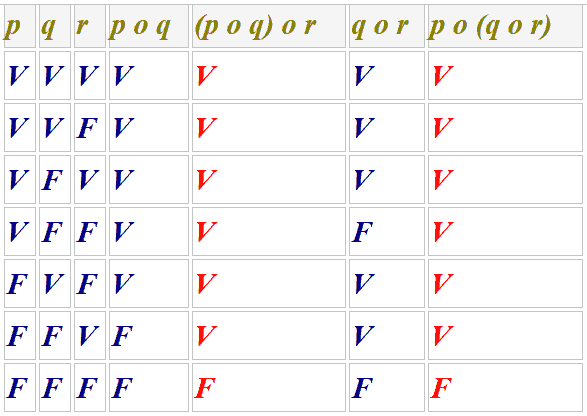
PROPRIETA' ASSOCIATIVA DEL PRODOTTO LOGICO:

PROPRIETA' DISTRIBUTIVA DELLA SOMMA LOGICA rispetto al PRODOTTO PRODOTTO LOGICO:

PROPRIETA' DISTRIBUTIVA DEL PRODOTTO LOGICO rispetto alla SOMMA LOGICA:

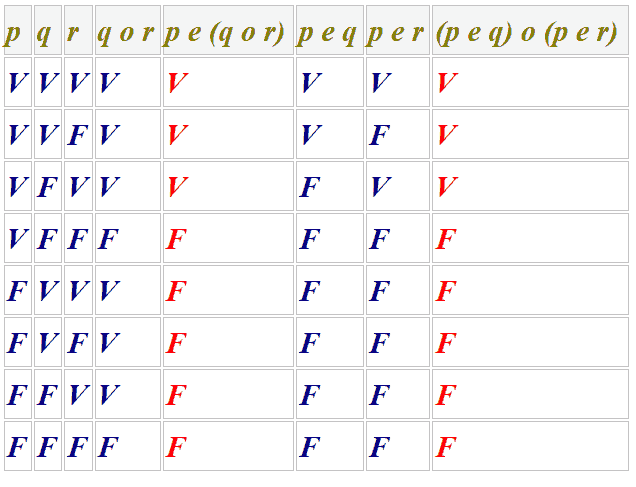
LEGGE DI ASSORBIMENTO DELLA SOMMA LOGICA:

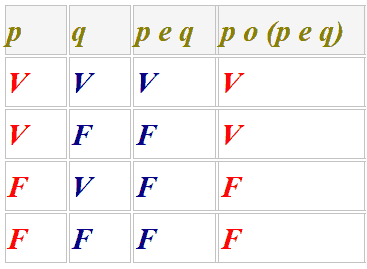
LEGGE DI ASSORBIMENTO DELLA SOMMA LOGICA:

Indice degli argomenti sulla logica matematica

Pubblicità/Advertising